Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 49200 by rahul 19 last updated on 04/Dec/18

1)Find the area of the triangle formed by roots of cubic equation (z+αb)^3 =α^3_ (α≠0). 2) Find product of all possible values of ((1/2)+(((√3)i)/2))^(3/4) .

$$\left.\mathrm{1}\right){Find}\:{the}\:{area}\:{of}\:{the}\:{triangle}\:{formed} \\ $$$${by}\:{roots}\:{of}\:{cubic}\:{equation} \\ $$$$\left({z}+\alpha{b}\right)^{\mathrm{3}} =\alpha^{\mathrm{3}_{} } \:\:\left(\alpha\neq\mathrm{0}\right). \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:{Find}\:{product}\:{of}\:{all}\:{possible}\:{values} \\ $$$${of}\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} \:. \\ $$

Commented by rahul 19 last updated on 04/Dec/18

Ans→1) 1.3 α^2 ... 2) 1 ...

$$\left.{Ans}\rightarrow\mathrm{1}\right)\:\mathrm{1}.\mathrm{3}\:\alpha^{\mathrm{2}} ... \\ $$$$\left.\mathrm{2}\right)\:\mathrm{1}\:... \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Dec/18

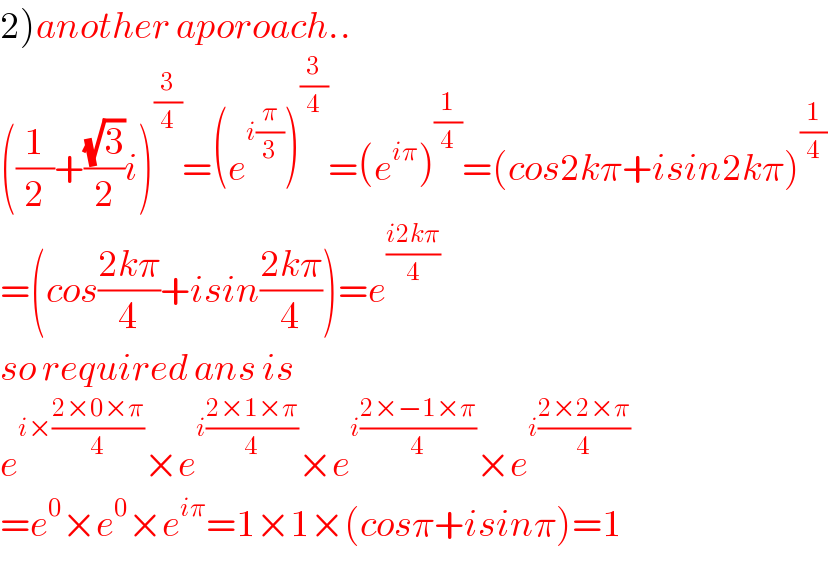
2)another aporoach.. ((1/2)+((√3)/2)i)^(3/4) =(e^(i(π/3)) )^(3/4) =(e^(iπ) )^(1/4) =(cos2kπ+isin2kπ)^(1/4) =(cos((2kπ)/4)+isin((2kπ)/4))=e^((i2kπ)/4) so required ans is e^(i×((2×0×π)/4)) ×e^(i((2×1×π)/4)) ×e^(i((2×−1×π)/4)) ×e^(i((2×2×π)/4)) =e^0 ×e^0 ×e^(iπ) =1×1×(cosπ+isinπ)=1

$$\left.\mathrm{2}\right){another}\:{aporoach}.. \\ $$$$\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} =\left({e}^{{i}\frac{\pi}{\mathrm{3}}} \right)^{\frac{\mathrm{3}}{\mathrm{4}}} =\left({e}^{{i}\pi} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} =\left({cos}\mathrm{2}{k}\pi+{isin}\mathrm{2}{k}\pi\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$=\left({cos}\frac{\mathrm{2}{k}\pi}{\mathrm{4}}+{isin}\frac{\mathrm{2}{k}\pi}{\mathrm{4}}\right)={e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{4}}} \\ $$$${so}\:{required}\:{ans}\:{is} \\ $$$${e}^{{i}×\frac{\mathrm{2}×\mathrm{0}×\pi}{\mathrm{4}}} ×{e}^{{i}\frac{\mathrm{2}×\mathrm{1}×\pi}{\mathrm{4}}} ×{e}^{{i}\frac{\mathrm{2}×−\mathrm{1}×\pi}{\mathrm{4}}} ×{e}^{{i}\frac{\mathrm{2}×\mathrm{2}×\pi}{\mathrm{4}}} \\ $$$$={e}^{\mathrm{0}} ×{e}^{\mathrm{0}} ×{e}^{{i}\pi} =\mathrm{1}×\mathrm{1}×\left({cos}\pi+{isin}\pi\right)=\mathrm{1} \\ $$

Commented by rahul 19 last updated on 05/Dec/18

cos π =−1 , right? So your answer comes out to be −1... Thank you sir for providing hint i ′ve got the correct ans. now :)

$$\mathrm{cos}\:\pi\:=−\mathrm{1}\:,\:{right}? \\ $$$${So}\:{your}\:{answer}\:{comes}\:{out}\:{to}\:{be}\:−\mathrm{1}... \\ $$$${Thank}\:{you}\:{sir}\:{for}\:{providing}\:{hint}\:{i}\:'{ve}\: \\ $$$$\left.{got}\:{the}\:{correct}\:{ans}.\:{now}\::\right) \\ $$

Commented by rahul 19 last updated on 05/Dec/18

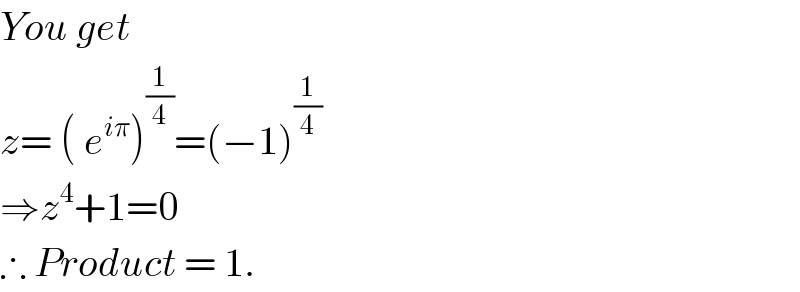
You get z= ( e^(iπ) )^(1/4) =(−1)^(1/4) ⇒z^4 +1=0 ∴ Product = 1.

$${You}\:{get}\: \\ $$$${z}=\:\left(\:{e}^{{i}\pi} \right)^{\frac{\mathrm{1}}{\mathrm{4}}} =\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\Rightarrow{z}^{\mathrm{4}} +\mathrm{1}=\mathrm{0}\: \\ $$$$\therefore\:{Product}\:=\:\mathrm{1}. \\ $$

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18

yes cosπ=−1 typo..

$${yes}\:{cos}\pi=−\mathrm{1}\:{typo}.. \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 04/Dec/18

1)(z+αb)^3 =α^3 ×1 (z+αb)^3 =α^3 ×e^(i2kπ) z+αb=α×e^((i2kπ)/3) z_1 +αb=α×e^((i×0×π)/3) =α(cos0^o +isin0^o ) (x_1 +iy_1 )+αb=α(1+i×0) (x_1 ,y_1 )={(α−αb),0}←A z_2 +αb=α×e^((i×2×1×π)/3) =α(cos120^o +isin120^o ) (x_2 +iy_2 )=−αb+α(((−1)/2)+((i×(√3))/2)) (x_2 ,y_2 )={(−αb−(α/2)),((α(√3))/2)}←B z_3 +αb=α×e^((i×2×−1×π)/3) =α(cos120^o −isin120^o ) (x_3 +iy_3 )+αb=α(((−1)/2)−((i(√3))/2)) (x_3 ,y_3 )={(−αb−(α/2)),((−α(√3))/2)}←C BC=α(√3) perpendicular distance from A to BC is α−αb+αb+(α/2)=((3α)/2) so area ABC=(1/2)×α(√3) ×((3α)/2)=((3(√3) α^2 )/4)=1.30α^2

$$\left.\mathrm{1}\right)\left({z}+\alpha{b}\right)^{\mathrm{3}} =\alpha^{\mathrm{3}} ×\mathrm{1} \\ $$$$\left({z}+\alpha{b}\right)^{\mathrm{3}} =\alpha^{\mathrm{3}} ×{e}^{{i}\mathrm{2}{k}\pi} \\ $$$${z}+\alpha{b}=\alpha×{e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{3}}} \\ $$$${z}_{\mathrm{1}} +\alpha{b}=\alpha×{e}^{\frac{{i}×\mathrm{0}×\pi}{\mathrm{3}}} =\alpha\left({cos}\mathrm{0}^{{o}} +{isin}\mathrm{0}^{{o}} \right) \\ $$$$\left({x}_{\mathrm{1}} +{iy}_{\mathrm{1}} \right)+\alpha{b}=\alpha\left(\mathrm{1}+{i}×\mathrm{0}\right) \\ $$$$\left({x}_{\mathrm{1}} ,{y}_{\mathrm{1}} \right)=\left\{\left(\alpha−\alpha{b}\right),\mathrm{0}\right\}\leftarrow{A} \\ $$$$ \\ $$$${z}_{\mathrm{2}} +\alpha{b}=\alpha×{e}^{\frac{{i}×\mathrm{2}×\mathrm{1}×\pi}{\mathrm{3}}} =\alpha\left({cos}\mathrm{120}^{{o}} +{isin}\mathrm{120}^{{o}} \right) \\ $$$$\left({x}_{\mathrm{2}} +{iy}_{\mathrm{2}} \right)=−\alpha{b}+\alpha\left(\frac{−\mathrm{1}}{\mathrm{2}}+\frac{{i}×\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right)=\left\{\left(−\alpha{b}−\frac{\alpha}{\mathrm{2}}\right),\frac{\alpha\sqrt{\mathrm{3}}}{\mathrm{2}}\right\}\leftarrow{B} \\ $$$${z}_{\mathrm{3}} +\alpha{b}=\alpha×{e}^{\frac{{i}×\mathrm{2}×−\mathrm{1}×\pi}{\mathrm{3}}} =\alpha\left({cos}\mathrm{120}^{{o}} −{isin}\mathrm{120}^{{o}} \right) \\ $$$$\left({x}_{\mathrm{3}} +{iy}_{\mathrm{3}} \right)+\alpha{b}=\alpha\left(\frac{−\mathrm{1}}{\mathrm{2}}−\frac{{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\left({x}_{\mathrm{3}} ,{y}_{\mathrm{3}} \right)=\left\{\left(−\alpha{b}−\frac{\alpha}{\mathrm{2}}\right),\frac{−\alpha\sqrt{\mathrm{3}}}{\mathrm{2}}\right\}\leftarrow{C} \\ $$$${BC}=\alpha\sqrt{\mathrm{3}}\: \\ $$$${perpendicular}\:{distance}\:{from}\:{A}\:{to}\:{BC}\:{is} \\ $$$$\alpha−\alpha{b}+\alpha{b}+\frac{\alpha}{\mathrm{2}}=\frac{\mathrm{3}\alpha}{\mathrm{2}} \\ $$$${so}\:{area}\:{ABC}=\frac{\mathrm{1}}{\mathrm{2}}×\alpha\sqrt{\mathrm{3}}\:×\frac{\mathrm{3}\alpha}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{3}}\:\alpha^{\mathrm{2}} }{\mathrm{4}}=\mathrm{1}.\mathrm{30}\alpha^{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by rahul 19 last updated on 05/Dec/18

thank you sir!���� colourful solñ!

Commented by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18

your posts are unique...

$${your}\:{posts}\:{are}\:{unique}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com