
Question Number 47239 by JDlix last updated on 06/Nov/18

$$\frac{\mathrm{1}.\mathrm{8}×\mathrm{10}^{\mathrm{6}} }{{tan}\left(\mathrm{89}.\mathrm{9999}°\right)}\:\sim\:\pi\:\left({upto}\:\mathrm{9}\:{decimal}\:{places}\right) \\ $$$${can}\:{i}\:{have}\:{some}\:{explanations}\:{how}\:{it}\:{is}\:{worked}\:{out}\:? \\ $$$${Thank}\:{you}! \\ $$
Commented by MJS last updated on 07/Nov/18

$$\mathrm{I}\:\mathrm{guess}\:\mathrm{somebody}\:\mathrm{just}\:\mathrm{messed}\:\mathrm{around}\:\mathrm{a}\:\mathrm{bit}. \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{find}\:\mathrm{many}\:\mathrm{almost}−\mathrm{identities} \\ $$$$\pi\mathrm{ln}\:\left(\pi\right)\:=\frac{\mathrm{143851}}{\mathrm{40000}}\:\left(\mathrm{error}\:\approx−\mathrm{2}.\mathrm{7}×\mathrm{10}^{−\mathrm{10}} \right) \\ $$$$\pi\mathrm{ln}\:\left(\pi\mathrm{ln}\:\left(\pi\right)\right)\:=\frac{\mathrm{100523}}{\mathrm{25000}}\:\left(\mathrm{error}\:\approx−\mathrm{2}.\mathrm{6}×\mathrm{10}^{−\mathrm{10}} \right) \\ $$$$\pi=\frac{\mathrm{6955380174}−\sqrt{\mathrm{3}}}{\mathrm{2213966271}}\:\left(\mathrm{error}\:\approx−\mathrm{5}×\mathrm{10}^{−\mathrm{13}} \right) \\ $$
Answered by MJS last updated on 07/Nov/18
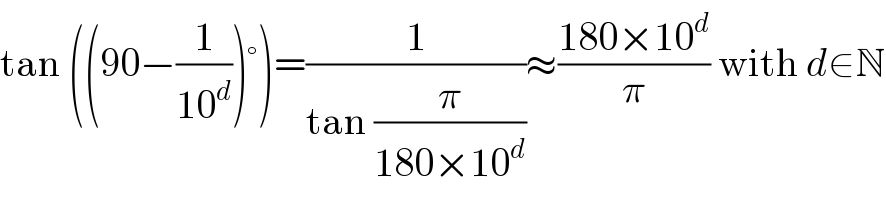
$$\mathrm{tan}\:\left(\left(\mathrm{90}−\frac{\mathrm{1}}{\mathrm{10}^{{d}} }\right)°\right)=\frac{\mathrm{1}}{\mathrm{tan}\:\frac{\pi}{\mathrm{180}×\mathrm{10}^{{d}} }}\approx\frac{\mathrm{180}×\mathrm{10}^{{d}} }{\pi}\:\mathrm{with}\:{d}\in\mathbb{N} \\ $$
