Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 155420 by amin96 last updated on 30/Sep/21

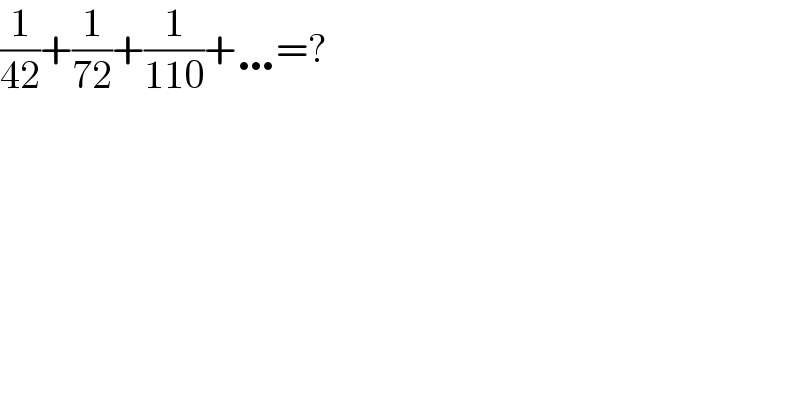
(1/(42))+(1/(72))+(1/(110))+…=?

$$\frac{\mathrm{1}}{\mathrm{42}}+\frac{\mathrm{1}}{\mathrm{72}}+\frac{\mathrm{1}}{\mathrm{110}}+\ldots=? \\ $$

Answered by puissant last updated on 01/Oct/21

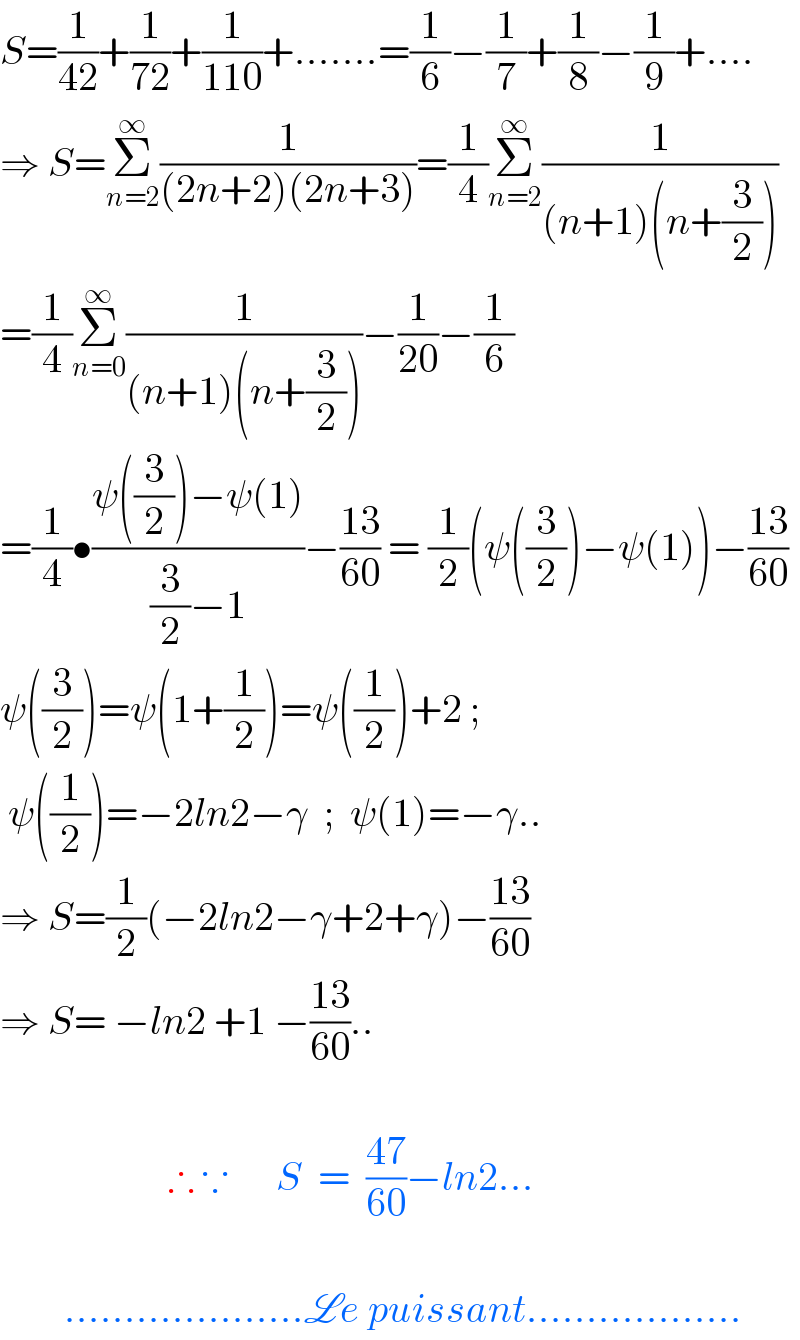
S=(1/(42))+(1/(72))+(1/(110))+.......=(1/6)−(1/7)+(1/8)−(1/9)+.... ⇒ S=Σ_(n=2) ^∞ (1/((2n+2)(2n+3)))=(1/4)Σ_(n=2) ^∞ (1/((n+1)(n+(3/2)))) =(1/4)Σ_(n=0) ^∞ (1/((n+1)(n+(3/2))))−(1/(20))−(1/6) =(1/4)•((ψ((3/2))−ψ(1))/((3/2)−1))−((13)/(60)) = (1/2)(ψ((3/2))−ψ(1))−((13)/(60)) ψ((3/2))=ψ(1+(1/2))=ψ((1/2))+2 ; ψ((1/2))=−2ln2−γ ; ψ(1)=−γ.. ⇒ S=(1/2)(−2ln2−γ+2+γ)−((13)/(60)) ⇒ S= −ln2 +1 −((13)/(60)).. ∴ ∵ S = ((47)/(60))−ln2... ....................Le puissant..................

$${S}=\frac{\mathrm{1}}{\mathrm{42}}+\frac{\mathrm{1}}{\mathrm{72}}+\frac{\mathrm{1}}{\mathrm{110}}+.......=\frac{\mathrm{1}}{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{9}}+.... \\ $$$$\Rightarrow\:{S}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{2}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)}=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}−\frac{\mathrm{1}}{\mathrm{20}}−\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\bullet\frac{\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\psi\left(\mathrm{1}\right)}{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}}−\frac{\mathrm{13}}{\mathrm{60}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\psi\left(\mathrm{1}\right)\right)−\frac{\mathrm{13}}{\mathrm{60}} \\ $$$$\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)=\psi\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{2}\:; \\ $$$$\:\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\mathrm{2}{ln}\mathrm{2}−\gamma\:\:;\:\:\psi\left(\mathrm{1}\right)=−\gamma.. \\ $$$$\Rightarrow\:{S}=\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{2}{ln}\mathrm{2}−\gamma+\mathrm{2}+\gamma\right)−\frac{\mathrm{13}}{\mathrm{60}} \\ $$$$\Rightarrow\:{S}=\:−{ln}\mathrm{2}\:+\mathrm{1}\:−\frac{\mathrm{13}}{\mathrm{60}}.. \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\therefore\:\because\:\:\:\:\:\:{S}\:\:=\:\:\frac{\mathrm{47}}{\mathrm{60}}−{ln}\mathrm{2}... \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:....................\mathscr{L}{e}\:{puissant}.................. \\ $$

Commented by amin96 last updated on 30/Sep/21

great sir

$${great}\:{sir} \\ $$

Commented by Tawa11 last updated on 30/Sep/21

Nice sir

$$\mathrm{Nice}\:\mathrm{sir} \\ $$

Commented by puissant last updated on 30/Sep/21

��������������

Commented by SANOGO last updated on 30/Sep/21

le puissant

$${le}\:{puissant} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com