
Question Number 142049 by mohammad17 last updated on 25/May/21

$$\int_{\mathrm{1}} ^{\:\mathrm{3}} {e}^{{x}^{\mathrm{2}} } {dx} \\ $$$${help}\:{me}\:{sir}\: \\ $$
Answered by Dwaipayan Shikari last updated on 26/May/21
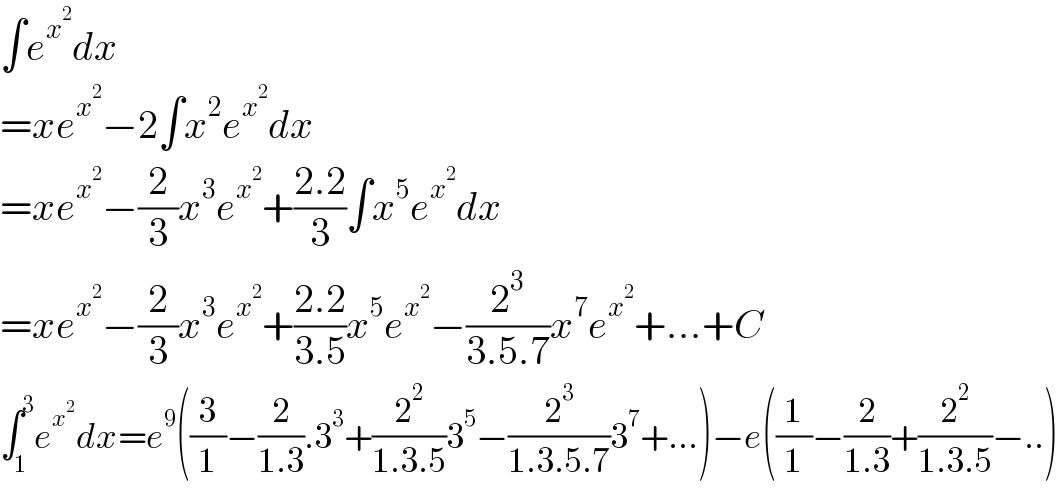
$$\int{e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$={xe}^{{x}^{\mathrm{2}} } −\mathrm{2}\int{x}^{\mathrm{2}} {e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$={xe}^{{x}^{\mathrm{2}} } −\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} {e}^{{x}^{\mathrm{2}} } +\frac{\mathrm{2}.\mathrm{2}}{\mathrm{3}}\int{x}^{\mathrm{5}} {e}^{{x}^{\mathrm{2}} } {dx} \\ $$$$={xe}^{{x}^{\mathrm{2}} } −\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} {e}^{{x}^{\mathrm{2}} } +\frac{\mathrm{2}.\mathrm{2}}{\mathrm{3}.\mathrm{5}}{x}^{\mathrm{5}} {e}^{{x}^{\mathrm{2}} } −\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}.\mathrm{5}.\mathrm{7}}{x}^{\mathrm{7}} {e}^{{x}^{\mathrm{2}} } +...+{C} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{3}} {e}^{{x}^{\mathrm{2}} } {dx}={e}^{\mathrm{9}} \left(\frac{\mathrm{3}}{\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{1}.\mathrm{3}}.\mathrm{3}^{\mathrm{3}} +\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{1}.\mathrm{3}.\mathrm{5}}\mathrm{3}^{\mathrm{5}} −\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}}\mathrm{3}^{\mathrm{7}} +...\right)−{e}\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{1}.\mathrm{3}}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{1}.\mathrm{3}.\mathrm{5}}−..\right) \\ $$
Answered by 676597498 last updated on 26/May/21
![I = ∫_(1 ) ^( 3) e^x^2 dx ⇒ I^2 = ∫_1 ^( 3) e^(x^2 +y^2 ) dxdy { ((r^2 =x^2 +y^2 )),( { ((x=rcosθ)),((y=rsinθ)) :}) :}⇒ I^2 =∫_1 ^( 3) e^r^2 rdrdθ { ((1 ≤ x ≤ 3)),((1 ≤ y ≤ 3)) :} ⇒ { ((x^2 ≤ 9)),((y^2 ≤ 9)) :}⇒ r^2 ≤ 18⇒ 0 ≤ r ≤ 3(√2) ⇒ I^2 = ∫_0 ^( 3(√2)) (∫_0 ^( 2π) dθ)re^r^2 dr ⇒ I^2 = 2π∫_0 ^( 3(√2)) re^r^2 dr = 2π[(e^r^2 /2)]_0 ^(3(√2)) ⇒ I^2 = 2π [(e^(18) /2)−1]=π(e^(18) −2) ⇒ ∫_1 ^( 3) e^x^2 dx = (√π).(√(e^(18) −2))](Q142137.png)
$${I}\:=\:\int_{\mathrm{1}\:} ^{\:\mathrm{3}} {e}^{{x}^{\mathrm{2}} } {dx}\:\Rightarrow\:{I}^{\mathrm{2}} \:=\:\int_{\mathrm{1}} ^{\:\mathrm{3}} {e}^{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } {dxdy} \\ $$$$\begin{cases}{{r}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} }\\{\begin{cases}{{x}={rcos}\theta}\\{{y}={rsin}\theta}\end{cases}}\end{cases}\Rightarrow\:{I}^{\mathrm{2}} =\int_{\mathrm{1}} ^{\:\mathrm{3}} {e}^{{r}^{\mathrm{2}} } {rdrd}\theta \\ $$$$\begin{cases}{\mathrm{1}\:\leqslant\:{x}\:\leqslant\:\mathrm{3}}\\{\mathrm{1}\:\leqslant\:{y}\:\leqslant\:\mathrm{3}}\end{cases}\:\Rightarrow\:\begin{cases}{{x}^{\mathrm{2}} \:\leqslant\:\mathrm{9}}\\{{y}^{\mathrm{2}} \:\leqslant\:\mathrm{9}}\end{cases}\Rightarrow\:{r}^{\mathrm{2}} \:\leqslant\:\mathrm{18}\Rightarrow\:\mathrm{0}\:\leqslant\:{r}\:\leqslant\:\mathrm{3}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\:{I}^{\mathrm{2}} \:=\:\int_{\mathrm{0}} ^{\:\mathrm{3}\sqrt{\mathrm{2}}} \left(\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} {d}\theta\right){re}^{{r}^{\mathrm{2}} } {dr} \\ $$$$\Rightarrow\:{I}^{\mathrm{2}} \:=\:\mathrm{2}\pi\int_{\mathrm{0}} ^{\:\mathrm{3}\sqrt{\mathrm{2}}} {re}^{{r}^{\mathrm{2}} } {dr}\:=\:\mathrm{2}\pi\left[\frac{{e}^{{r}^{\mathrm{2}} } }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\:{I}^{\mathrm{2}} \:=\:\mathrm{2}\pi\:\left[\frac{{e}^{\mathrm{18}} }{\mathrm{2}}−\mathrm{1}\right]=\pi\left({e}^{\mathrm{18}} −\mathrm{2}\right) \\ $$$$\Rightarrow\:\int_{\mathrm{1}} ^{\:\mathrm{3}} {e}^{{x}^{\mathrm{2}} } {dx}\:=\:\sqrt{\pi}.\sqrt{{e}^{\mathrm{18}} −\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 27/May/21
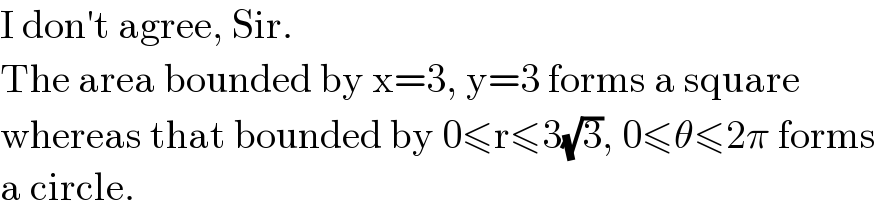
$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{agree},\:\mathrm{Sir}.\: \\ $$$$\mathrm{The}\:\mathrm{area}\:\mathrm{bounded}\:\mathrm{by}\:\mathrm{x}=\mathrm{3},\:\mathrm{y}=\mathrm{3}\:\mathrm{forms}\:\mathrm{a}\:\mathrm{square} \\ $$$$\mathrm{whereas}\:\mathrm{that}\:\mathrm{bounded}\:\mathrm{by}\:\mathrm{0}\leqslant\mathrm{r}\leqslant\mathrm{3}\sqrt{\mathrm{3}},\:\mathrm{0}\leqslant\theta\leqslant\mathrm{2}\pi\:\mathrm{forms} \\ $$$$\mathrm{a}\:\mathrm{circle}.\: \\ $$
