Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 130748 by Dwaipayan Shikari last updated on 28/Jan/21

(1/3^3 )−(1/5^3 )+(1/(11^3 ))−(1/(13^3 ))+(1/(19^3 ))−(1/(21^3 ))+(1/(29^3 ))−(1/(31^3 ))+..

$$\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{11}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{13}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{19}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{21}^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{29}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{31}^{\mathrm{3}} }+.. \\ $$

Answered by mindispower last updated on 28/Jan/21

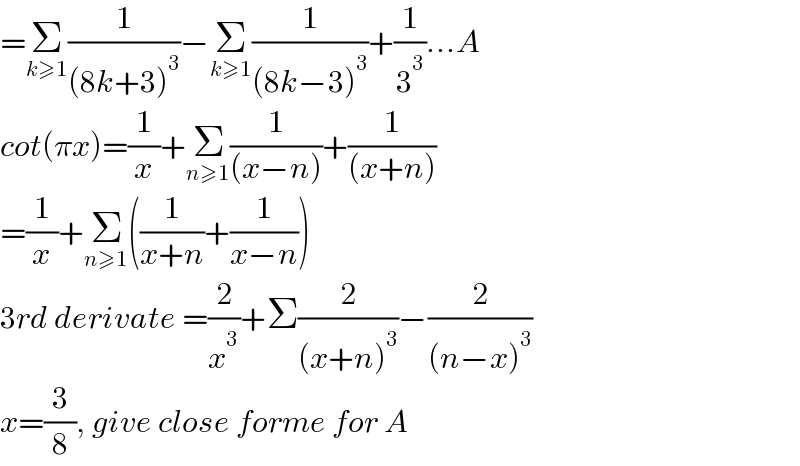
=Σ_(k≥1) (1/((8k+3)^3 ))−Σ_(k≥1) (1/((8k−3)^3 ))+(1/3^3 )...A cot(πx)=(1/x)+Σ_(n≥1) (1/((x−n)))+(1/((x+n))) =(1/x)+Σ_(n≥1) ((1/(x+n))+(1/(x−n))) 3rd derivate =(2/x^3 )+Σ(2/((x+n)^3 ))−(2/((n−x)^3 )) x=(3/8), give close forme for A

$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{8}{k}+\mathrm{3}\right)^{\mathrm{3}} }−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{8}{k}−\mathrm{3}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }...{A} \\ $$$${cot}\left(\pi{x}\right)=\frac{\mathrm{1}}{{x}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({x}−{n}\right)}+\frac{\mathrm{1}}{\left({x}+{n}\right)} \\ $$$$=\frac{\mathrm{1}}{{x}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\left(\frac{\mathrm{1}}{{x}+{n}}+\frac{\mathrm{1}}{{x}−{n}}\right) \\ $$$$\mathrm{3}{rd}\:{derivate}\:=\frac{\mathrm{2}}{{x}^{\mathrm{3}} }+\Sigma\frac{\mathrm{2}}{\left({x}+{n}\right)^{\mathrm{3}} }−\frac{\mathrm{2}}{\left({n}−{x}\right)^{\mathrm{3}} } \\ $$$${x}=\frac{\mathrm{3}}{\mathrm{8}},\:{give}\:{close}\:{forme}\:{for}\:{A} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com