Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 166468 by mathlove last updated on 20/Feb/22

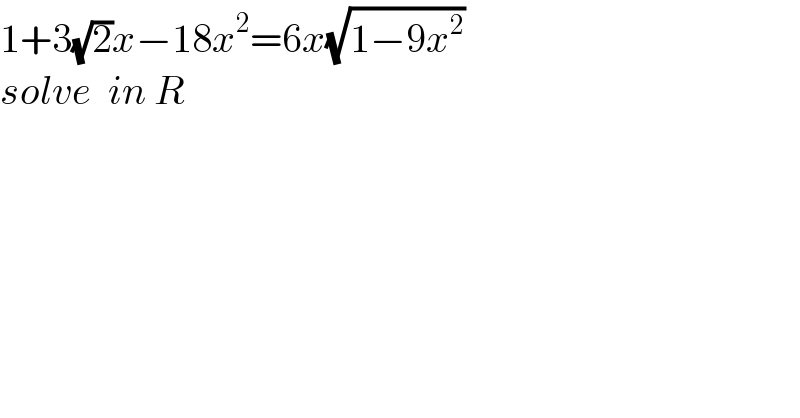
1+3(√2)x−18x^2 =6x(√(1−9x^2 )) solve in R

$$\mathrm{1}+\mathrm{3}\sqrt{\mathrm{2}}{x}−\mathrm{18}{x}^{\mathrm{2}} =\mathrm{6}{x}\sqrt{\mathrm{1}−\mathrm{9}{x}^{\mathrm{2}} } \\ $$$${solve}\:\:{in}\:{R} \\ $$

Answered by MJS_new last updated on 20/Feb/22

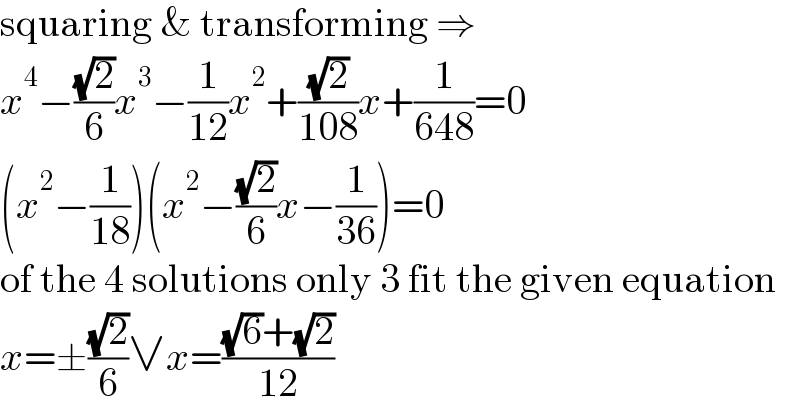
squaring & transforming ⇒ x^4 −((√2)/6)x^3 −(1/(12))x^2 +((√2)/(108))x+(1/(648))=0 (x^2 −(1/(18)))(x^2 −((√2)/6)x−(1/(36)))=0 of the 4 solutions only 3 fit the given equation x=±((√2)/6)∨x=(((√6)+(√2))/(12))

$$\mathrm{squaring}\:\&\:\mathrm{transforming}\:\Rightarrow \\ $$$${x}^{\mathrm{4}} −\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{12}}{x}^{\mathrm{2}} +\frac{\sqrt{\mathrm{2}}}{\mathrm{108}}{x}+\frac{\mathrm{1}}{\mathrm{648}}=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{18}}\right)\left({x}^{\mathrm{2}} −\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}{x}−\frac{\mathrm{1}}{\mathrm{36}}\right)=\mathrm{0} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{4}\:\mathrm{solutions}\:\mathrm{only}\:\mathrm{3}\:\mathrm{fit}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$${x}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\vee{x}=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{12}} \\ $$

Answered by mr W last updated on 20/Feb/22

let 3x=sin θ 1+(√2) sin θ−2 sin^2 θ=2 sin θ cos θ cos 2θ+(√2) sin θ=sin 2θ sin θ=(1/( (√2)))(sin 2θ−cos 2θ) sin θ=sin (2θ−(π/4)) 2θ−(π/4)=2kπ+θ ⇒θ=2kπ+(π/4) 2θ−(π/4)=(2k+1)π−θ ⇒θ=((2kπ)/3)+((5π)/(12)) ⇒x_1 =(1/3) sin (π/4)=((√2)/6) ⇒x_2 =(1/3) sin ((5π)/(12))=(((√6)+(√2))/(12)) ⇒x_3 =−(1/3) sin ((π/4))=−((√2)/6) ⇒x=(1/3) sin (((13π)/(12))) (rejected, since cos ((13π)/(12))<0)

$${let}\:\mathrm{3}{x}=\mathrm{sin}\:\theta \\ $$$$\mathrm{1}+\sqrt{\mathrm{2}}\:\mathrm{sin}\:\theta−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\theta=\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta \\ $$$$\mathrm{cos}\:\mathrm{2}\theta+\sqrt{\mathrm{2}}\:\mathrm{sin}\:\theta=\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\mathrm{sin}\:\theta=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{sin}\:\mathrm{2}\theta−\mathrm{cos}\:\mathrm{2}\theta\right) \\ $$$$\mathrm{sin}\:\theta=\mathrm{sin}\:\left(\mathrm{2}\theta−\frac{\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{2}\theta−\frac{\pi}{\mathrm{4}}=\mathrm{2}{k}\pi+\theta\:\Rightarrow\theta=\mathrm{2}{k}\pi+\frac{\pi}{\mathrm{4}} \\ $$$$\mathrm{2}\theta−\frac{\pi}{\mathrm{4}}=\left(\mathrm{2}{k}+\mathrm{1}\right)\pi−\theta\:\Rightarrow\theta=\frac{\mathrm{2}{k}\pi}{\mathrm{3}}+\frac{\mathrm{5}\pi}{\mathrm{12}} \\ $$$$\Rightarrow{x}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}\:\frac{\pi}{\mathrm{4}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{6}} \\ $$$$\Rightarrow{x}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}\:\frac{\mathrm{5}\pi}{\mathrm{12}}=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{12}} \\ $$$$\Rightarrow{x}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}\right)=−\frac{\sqrt{\mathrm{2}}}{\mathrm{6}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{3}}\:\mathrm{sin}\:\left(\frac{\mathrm{13}\pi}{\mathrm{12}}\right)\:\left({rejected},\:{since}\:\mathrm{cos}\:\frac{\mathrm{13}\pi}{\mathrm{12}}<\mathrm{0}\right) \\ $$

Commented by peter frank last updated on 20/Feb/22

Thank you both

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{both} \\ $$

Commented by MaxiMaths last updated on 20/Feb/22

ok

$$\mathrm{ok} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com