Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 215845 by Tawa11 last updated on 19/Jan/25

1, 3, − 1, − 3, − 7, − 21, − 25, ___, ___, ___ Next three terms??

$$\mathrm{1},\:\mathrm{3},\:−\:\mathrm{1},\:−\:\mathrm{3},\:−\:\mathrm{7},\:\:−\:\mathrm{21},\:\:−\:\mathrm{25},\:\:\:\:\:\_\_\_,\:\:\:\:\:\_\_\_,\:\:\:\:\:\_\_\_ \\ $$$$ \\ $$$$\mathrm{Next}\:\mathrm{three}\:\mathrm{terms}?? \\ $$

Commented by mr W last updated on 20/Jan/25

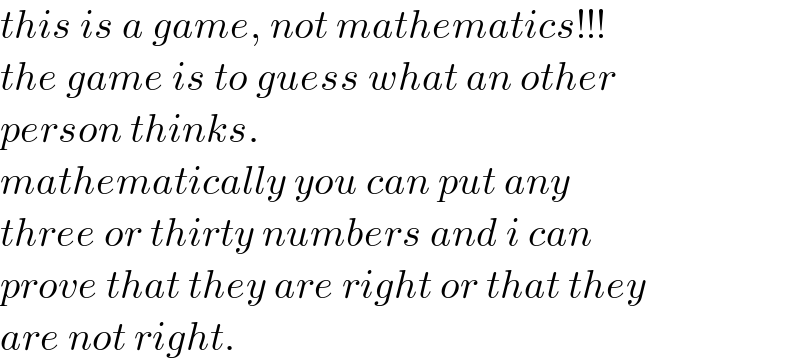
this is a game, not mathematics!!! the game is to guess what an other person thinks. mathematically you can put any three or thirty numbers and i can prove that they are right or that they are not right.

$${this}\:{is}\:{a}\:{game},\:{not}\:{mathematics}!!! \\ $$$${the}\:{game}\:{is}\:{to}\:{guess}\:{what}\:{an}\:{other} \\ $$$${person}\:{thinks}.\: \\ $$$${mathematically}\:{you}\:{can}\:{put}\:{any} \\ $$$${three}\:{or}\:{thirty}\:{numbers}\:{and}\:{i}\:{can} \\ $$$${prove}\:{that}\:{they}\:{are}\:{right}\:{or}\:{that}\:{they} \\ $$$${are}\:{not}\:{right}. \\ $$

Commented by mr W last updated on 20/Jan/25

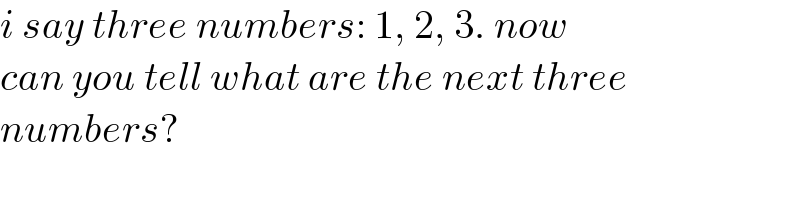
i say three numbers: 1, 2, 3. now can you tell what are the next three numbers?

$${i}\:{say}\:{three}\:{numbers}:\:\mathrm{1},\:\mathrm{2},\:\mathrm{3}.\:{now}\: \\ $$$${can}\:{you}\:{tell}\:{what}\:{are}\:{the}\:{next}\:{three} \\ $$$${numbers}? \\ $$

Commented by Tawa11 last updated on 20/Jan/25

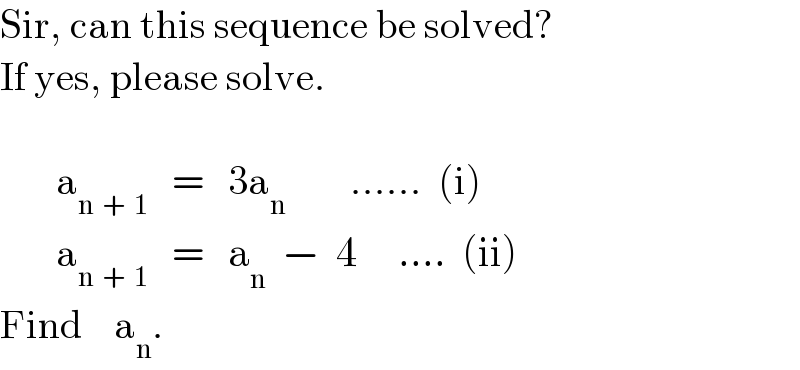
Sir, can this sequence be solved? If yes, please solve. a_(n + 1) = 3a_n ...... (i) a_(n + 1) = a_n − 4 .... (ii) Find a_n .

$$\mathrm{Sir},\:\mathrm{can}\:\mathrm{this}\:\mathrm{sequence}\:\mathrm{be}\:\mathrm{solved}? \\ $$$$\mathrm{If}\:\mathrm{yes},\:\mathrm{please}\:\mathrm{solve}. \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\mathrm{a}_{\mathrm{n}\:\:+\:\:\mathrm{1}} \:\:\:=\:\:\:\mathrm{3a}_{\mathrm{n}} \:\:\:\:\:\:\:\:......\:\:\left(\mathrm{i}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{a}_{\mathrm{n}\:\:+\:\:\mathrm{1}} \:\:\:=\:\:\:\mathrm{a}_{\mathrm{n}} \:\:−\:\:\mathrm{4}\:\:\:\:\:....\:\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{Find}\:\:\:\:\mathrm{a}_{\mathrm{n}} . \\ $$

Commented by mr W last updated on 20/Jan/25

you mean the question is a_0 =1 a_(n+1) =3a_n , if n is even a_(n+1) =a_n −4, if n is odd find a_n =?

$${you}\:{mean}\:{the}\:{question}\:{is} \\ $$$${a}_{\mathrm{0}} =\mathrm{1} \\ $$$${a}_{{n}+\mathrm{1}} =\mathrm{3}{a}_{{n}} ,\:{if}\:{n}\:{is}\:{even} \\ $$$${a}_{{n}+\mathrm{1}} ={a}_{{n}} −\mathrm{4},\:\:{if}\:{n}\:{is}\:{odd} \\ $$$${find}\:{a}_{{n}} =? \\ $$

Commented by Tawa11 last updated on 20/Jan/25

Yes sir. Exactly.

$$\mathrm{Yes}\:\mathrm{sir}.\:\mathrm{Exactly}. \\ $$

Commented by mr W last updated on 20/Jan/25

{ ((a_(2k) =2−3^k )),((a_(2k+1) =3(2−3^k ))) :}

$$\begin{cases}{{a}_{\mathrm{2}{k}} =\mathrm{2}−\mathrm{3}^{{k}} }\\{{a}_{\mathrm{2}{k}+\mathrm{1}} =\mathrm{3}\left(\mathrm{2}−\mathrm{3}^{{k}} \right)}\end{cases} \\ $$

Commented by mr W last updated on 20/Jan/25

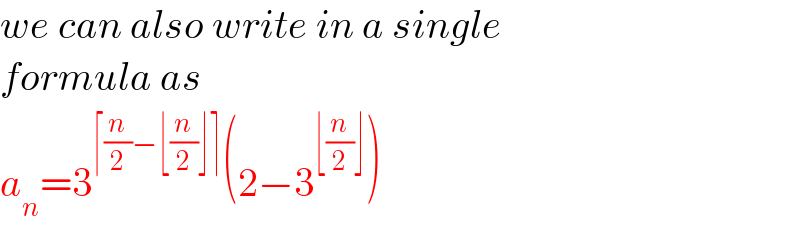
we can also write in a single formula as a_n =3^(⌈(n/2)−⌊(n/2)⌋⌉) (2−3^(⌊(n/2)⌋) )

$${we}\:{can}\:{also}\:{write}\:{in}\:{a}\:{single}\: \\ $$$${formula}\:{as} \\ $$$${a}_{{n}} =\mathrm{3}^{\lceil\frac{{n}}{\mathrm{2}}−\lfloor\frac{{n}}{\mathrm{2}}\rfloor\rceil} \left(\mathrm{2}−\mathrm{3}^{\lfloor\frac{{n}}{\mathrm{2}}\rfloor} \right) \\ $$

Commented by Tawa11 last updated on 20/Jan/25

What does the bracket signify sir. And do you combine it sir.?

$$\mathrm{What}\:\mathrm{does}\:\mathrm{the}\:\mathrm{bracket}\:\mathrm{signify}\:\mathrm{sir}. \\ $$$$\mathrm{And}\:\mathrm{do}\:\mathrm{you}\:\mathrm{combine}\:\mathrm{it}\:\mathrm{sir}.? \\ $$

Commented by mr W last updated on 20/Jan/25

https://en.m.wikipedia.org/wiki/Floor_and_ceiling_functions

Commented by Tawa11 last updated on 20/Jan/25

Thanks sir.

$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$

Answered by Tawa11 last updated on 19/Jan/25

Commented by Tawa11 last updated on 19/Jan/25

1 × 3 = 3 first term by 3 to give second, then 3 - 4 = -1 to give the third. -1 × 3 = -3 (4th) -3 - 4 = -7 (5th) -7 × 3 = -21 etc

1 × 3 = 3 first term by 3 to give second, then 3 - 4 = -1 to give the third. -1 × 3 = -3 (4th) -3 - 4 = -7 (5th) -7 × 3 = -21 etc

Answered by mr W last updated on 20/Jan/25

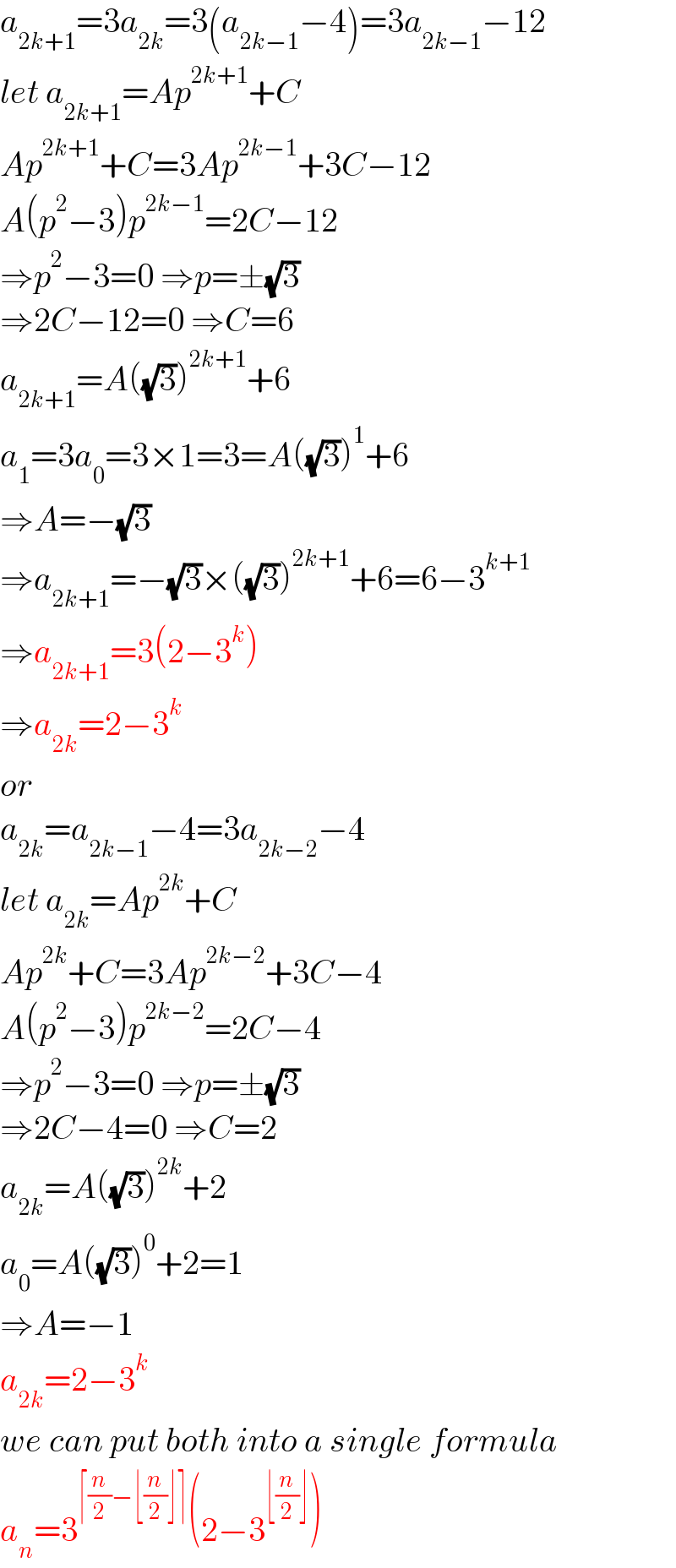
a_(2k+1) =3a_(2k) =3(a_(2k−1) −4)=3a_(2k−1) −12 let a_(2k+1) =Ap^(2k+1) +C Ap^(2k+1) +C=3Ap^(2k−1) +3C−12 A(p^2 −3)p^(2k−1) =2C−12 ⇒p^2 −3=0 ⇒p=±(√3) ⇒2C−12=0 ⇒C=6 a_(2k+1) =A((√3))^(2k+1) +6 a_1 =3a_0 =3×1=3=A((√3))^1 +6 ⇒A=−(√3) ⇒a_(2k+1) =−(√3)×((√3))^(2k+1) +6=6−3^(k+1) ⇒a_(2k+1) =3(2−3^k ) ⇒a_(2k) =2−3^k or a_(2k) =a_(2k−1) −4=3a_(2k−2) −4 let a_(2k) =Ap^(2k) +C Ap^(2k) +C=3Ap^(2k−2) +3C−4 A(p^2 −3)p^(2k−2) =2C−4 ⇒p^2 −3=0 ⇒p=±(√3) ⇒2C−4=0 ⇒C=2 a_(2k) =A((√3))^(2k) +2 a_0 =A((√3))^0 +2=1 ⇒A=−1 a_(2k) =2−3^k we can put both into a single formula a_n =3^(⌈(n/2)−⌊(n/2)⌋⌉) (2−3^(⌊(n/2)⌋) )

$${a}_{\mathrm{2}{k}+\mathrm{1}} =\mathrm{3}{a}_{\mathrm{2}{k}} =\mathrm{3}\left({a}_{\mathrm{2}{k}−\mathrm{1}} −\mathrm{4}\right)=\mathrm{3}{a}_{\mathrm{2}{k}−\mathrm{1}} −\mathrm{12} \\ $$$${let}\:{a}_{\mathrm{2}{k}+\mathrm{1}} ={Ap}^{\mathrm{2}{k}+\mathrm{1}} +{C} \\ $$$${Ap}^{\mathrm{2}{k}+\mathrm{1}} +{C}=\mathrm{3}{Ap}^{\mathrm{2}{k}−\mathrm{1}} +\mathrm{3}{C}−\mathrm{12} \\ $$$${A}\left({p}^{\mathrm{2}} −\mathrm{3}\right){p}^{\mathrm{2}{k}−\mathrm{1}} =\mathrm{2}{C}−\mathrm{12} \\ $$$$\Rightarrow{p}^{\mathrm{2}} −\mathrm{3}=\mathrm{0}\:\Rightarrow{p}=\pm\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2}{C}−\mathrm{12}=\mathrm{0}\:\Rightarrow{C}=\mathrm{6} \\ $$$${a}_{\mathrm{2}{k}+\mathrm{1}} ={A}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}{k}+\mathrm{1}} +\mathrm{6} \\ $$$${a}_{\mathrm{1}} =\mathrm{3}{a}_{\mathrm{0}} =\mathrm{3}×\mathrm{1}=\mathrm{3}={A}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{1}} +\mathrm{6} \\ $$$$\Rightarrow{A}=−\sqrt{\mathrm{3}} \\ $$$$\Rightarrow{a}_{\mathrm{2}{k}+\mathrm{1}} =−\sqrt{\mathrm{3}}×\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}{k}+\mathrm{1}} +\mathrm{6}=\mathrm{6}−\mathrm{3}^{{k}+\mathrm{1}} \\ $$$$\Rightarrow{a}_{\mathrm{2}{k}+\mathrm{1}} =\mathrm{3}\left(\mathrm{2}−\mathrm{3}^{{k}} \right) \\ $$$$\Rightarrow{a}_{\mathrm{2}{k}} =\mathrm{2}−\mathrm{3}^{{k}} \\ $$$${or} \\ $$$${a}_{\mathrm{2}{k}} ={a}_{\mathrm{2}{k}−\mathrm{1}} −\mathrm{4}=\mathrm{3}{a}_{\mathrm{2}{k}−\mathrm{2}} −\mathrm{4} \\ $$$${let}\:{a}_{\mathrm{2}{k}} ={Ap}^{\mathrm{2}{k}} +{C} \\ $$$${Ap}^{\mathrm{2}{k}} +{C}=\mathrm{3}{Ap}^{\mathrm{2}{k}−\mathrm{2}} +\mathrm{3}{C}−\mathrm{4} \\ $$$${A}\left({p}^{\mathrm{2}} −\mathrm{3}\right){p}^{\mathrm{2}{k}−\mathrm{2}} =\mathrm{2}{C}−\mathrm{4} \\ $$$$\Rightarrow{p}^{\mathrm{2}} −\mathrm{3}=\mathrm{0}\:\Rightarrow{p}=\pm\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{2}{C}−\mathrm{4}=\mathrm{0}\:\Rightarrow{C}=\mathrm{2} \\ $$$${a}_{\mathrm{2}{k}} ={A}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}{k}} +\mathrm{2} \\ $$$${a}_{\mathrm{0}} ={A}\left(\sqrt{\mathrm{3}}\right)^{\mathrm{0}} +\mathrm{2}=\mathrm{1}\: \\ $$$$\Rightarrow{A}=−\mathrm{1} \\ $$$${a}_{\mathrm{2}{k}} =\mathrm{2}−\mathrm{3}^{{k}} \\ $$$${we}\:{can}\:{put}\:{both}\:{into}\:{a}\:{single}\:{formula} \\ $$$${a}_{{n}} =\mathrm{3}^{\lceil\frac{{n}}{\mathrm{2}}−\lfloor\frac{{n}}{\mathrm{2}}\rfloor\rceil} \left(\mathrm{2}−\mathrm{3}^{\lfloor\frac{{n}}{\mathrm{2}}\rfloor} \right) \\ $$

Commented by Tawa11 last updated on 20/Jan/25

Wow, thanks sir. It works for the sequence.

$$\mathrm{Wow},\:\mathrm{thanks}\:\mathrm{sir}. \\ $$$$\mathrm{It}\:\mathrm{works}\:\mathrm{for}\:\mathrm{the}\:\mathrm{sequence}. \\ $$

Commented by Tawa11 last updated on 23/Jan/25

Sir mrW, sorry for calling you everytime for my question. Please help on the mechanics question I posted sir. Thanks always sir. Q215975

$$\mathrm{Sir}\:\mathrm{mrW},\:\mathrm{sorry}\:\mathrm{for}\:\mathrm{calling}\:\mathrm{you}\:\mathrm{everytime}\:\mathrm{for} \\ $$$$\mathrm{my}\:\mathrm{question}.\:\mathrm{Please}\:\mathrm{help}\:\mathrm{on}\:\mathrm{the}\:\mathrm{mechanics}\:\mathrm{question} \\ $$$$\mathrm{I}\:\mathrm{posted}\:\mathrm{sir}.\:\mathrm{Thanks}\:\mathrm{always}\:\mathrm{sir}.\:\:\:\mathrm{Q215975} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com