
Question Number 140890 by mathsuji last updated on 13/May/21
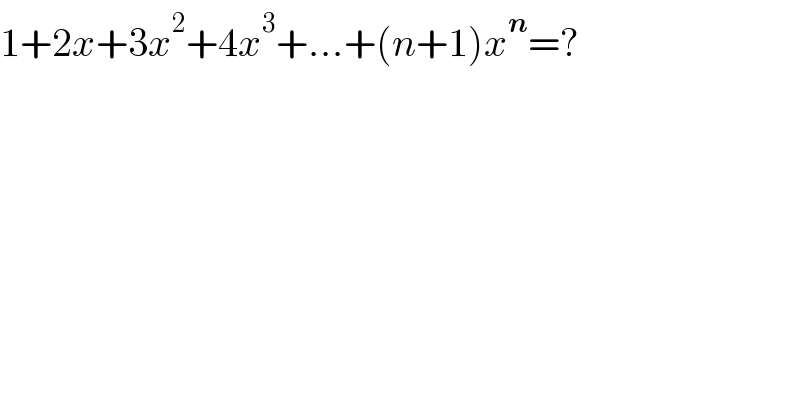
$$\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +...+\left({n}+\mathrm{1}\right){x}^{\boldsymbol{{n}}} =? \\ $$
Answered by ajfour last updated on 14/May/21
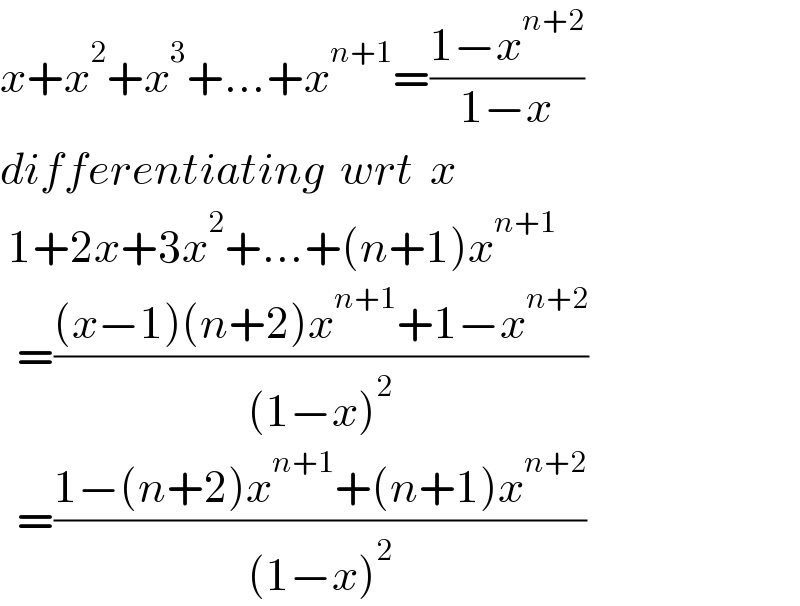
$${x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...+{x}^{{n}+\mathrm{1}} =\frac{\mathrm{1}−{x}^{{n}+\mathrm{2}} }{\mathrm{1}−{x}} \\ $$$${differentiating}\:\:{wrt}\:\:{x} \\ $$$$\:\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +...+\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} \\ $$$$\:\:=\frac{\left({x}−\mathrm{1}\right)\left({n}+\mathrm{2}\right){x}^{{n}+\mathrm{1}} +\mathrm{1}−{x}^{{n}+\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\:\:=\frac{\mathrm{1}−\left({n}+\mathrm{2}\right){x}^{{n}+\mathrm{1}} +\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }\: \\ $$
Commented by mathsuji last updated on 15/May/21

$${thaks}\:{Sir} \\ $$
