
Question Number 41651 by rahul 19 last updated on 10/Aug/18
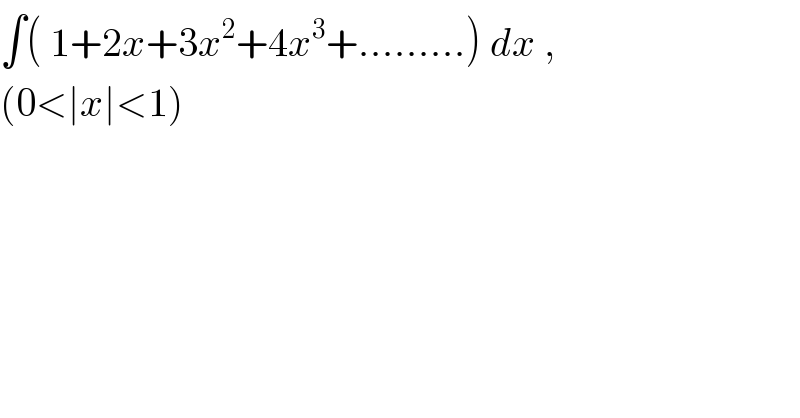
$$\int\left(\:\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +.........\right)\:{dx}\:,\:\:\: \\ $$$$\left(\mathrm{0}<\mid{x}\mid<\mathrm{1}\right) \\ $$
Commented by maxmathsup by imad last updated on 10/Aug/18
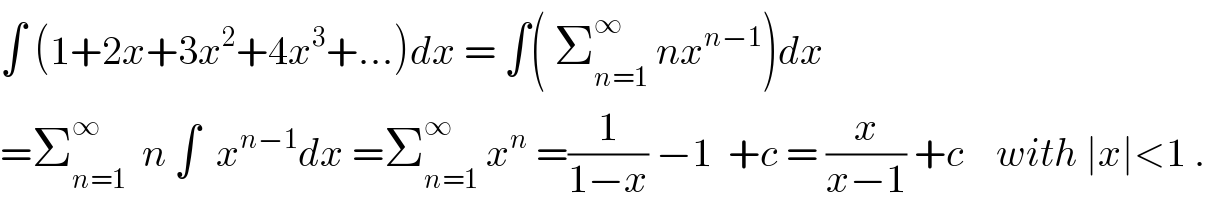
$$\int\:\left(\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +...\right){dx}\:=\:\int\left(\:\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \right){dx} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:{n}\:\int\:\:{x}^{{n}−\mathrm{1}} {dx}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:{x}^{{n}} \:=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:−\mathrm{1}\:\:+{c}\:=\:\frac{{x}}{{x}−\mathrm{1}}\:+{c}\:\:\:\:{with}\:\mid{x}\mid<\mathrm{1}\:. \\ $$
Answered by alex041103 last updated on 10/Aug/18
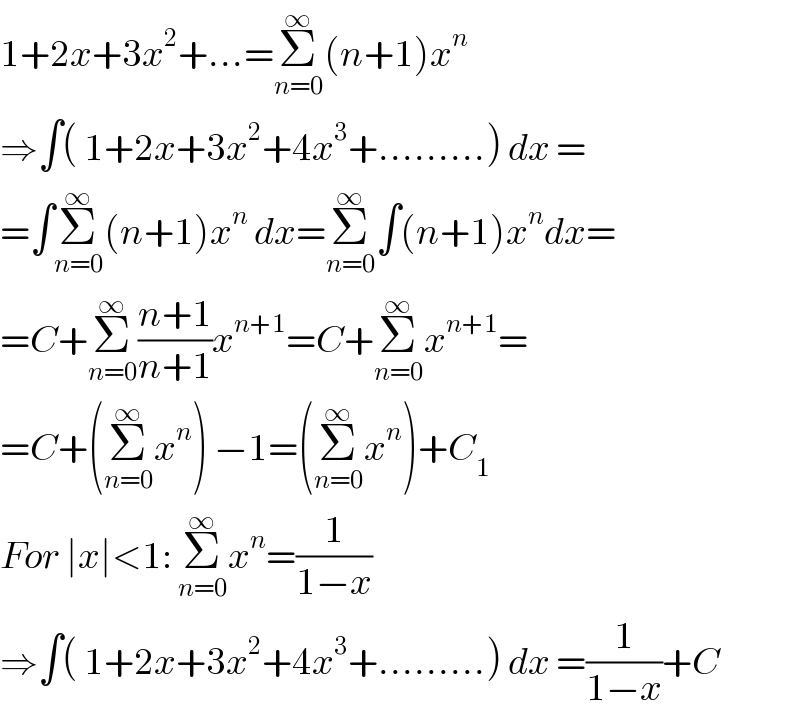
$$\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +...=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){x}^{{n}} \\ $$$$\Rightarrow\int\left(\:\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +.........\right)\:{dx}\:= \\ $$$$=\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left({n}+\mathrm{1}\right){x}^{{n}} \:{dx}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int\left({n}+\mathrm{1}\right){x}^{{n}} {dx}= \\ $$$$={C}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{n}+\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} ={C}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}+\mathrm{1}} = \\ $$$$={C}+\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \right)\:−\mathrm{1}=\left(\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} \right)+{C}_{\mathrm{1}} \\ $$$${For}\:\mid{x}\mid<\mathrm{1}:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\Rightarrow\int\left(\:\mathrm{1}+\mathrm{2}{x}+\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{3}} +.........\right)\:{dx}\:=\frac{\mathrm{1}}{\mathrm{1}−{x}}+{C} \\ $$
Commented by rahul 19 last updated on 10/Aug/18

$$\mathrm{thanks}\:\mathrm{sir}! \\ $$
Answered by rahul 19 last updated on 10/Aug/18
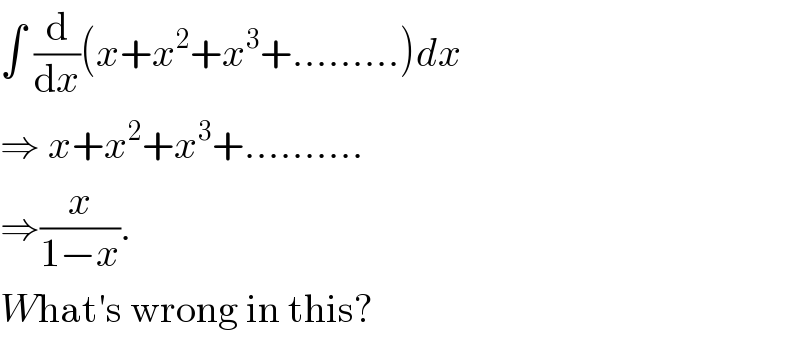
$$\int\:\frac{\mathrm{d}}{\mathrm{d}{x}}\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +.........\right){dx}\: \\ $$$$\Rightarrow\:{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +.......... \\ $$$$\Rightarrow\frac{{x}}{\mathrm{1}−{x}}. \\ $$$${W}\mathrm{hat}'\mathrm{s}\:\mathrm{wrong}\:\mathrm{in}\:\mathrm{this}? \\ $$
Commented by alex041103 last updated on 10/Aug/18

$${Nothing}\:{is}\:{wrong}.\:{If}\:{you}\:{look}\:{more} \\ $$$${carefully}\:{yoi}\:{will}\:{see}\:{that}: \\ $$$$\frac{{x}}{\mathrm{1}−{x}}=−\frac{\mathrm{1}−{x}\:−\mathrm{1}}{\mathrm{1}−{x}}=−\left(\frac{\mathrm{1}−{x}}{\mathrm{1}−{x}}−\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)= \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{x}}−\mathrm{1}=\frac{\mathrm{1}}{\mathrm{1}+{x}}+{C} \\ $$$${As}\:{you}\:{can}\:{see}\:{the}\:{integration}\:{constant} \\ $$$${is}\:{sth}\:{very}\:{imortant} \\ $$
Commented by rahul 19 last updated on 10/Aug/18
$$\mathrm{ohh},\:\mathrm{yes}\:\mathrm{u}\:\mathrm{r}\:\mathrm{right}\:\mathrm{sir}! \\ $$
