Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 64631 by Mikael last updated on 19/Jul/19

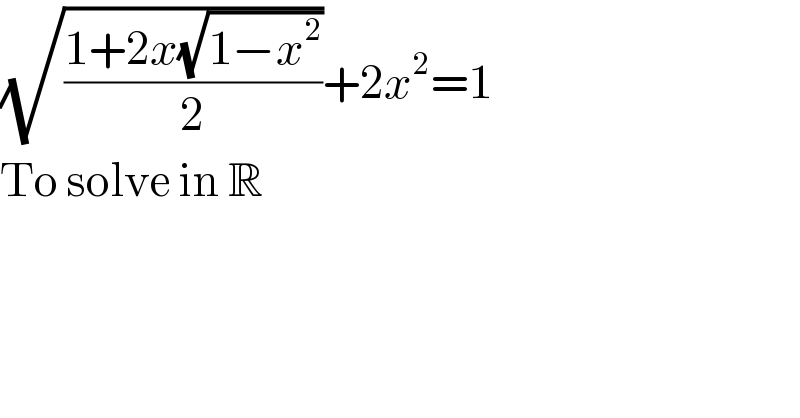
(√((1+2x(√(1−x^2 )))/2))+2x^2 =1 To solve in R

$$\sqrt{\frac{\mathrm{1}+\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{\mathrm{2}}}+\mathrm{2}{x}^{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{To}\:\mathrm{solve}\:\mathrm{in}\:\mathbb{R} \\ $$

Commented by behi83417@gmail.com last updated on 20/Jul/19

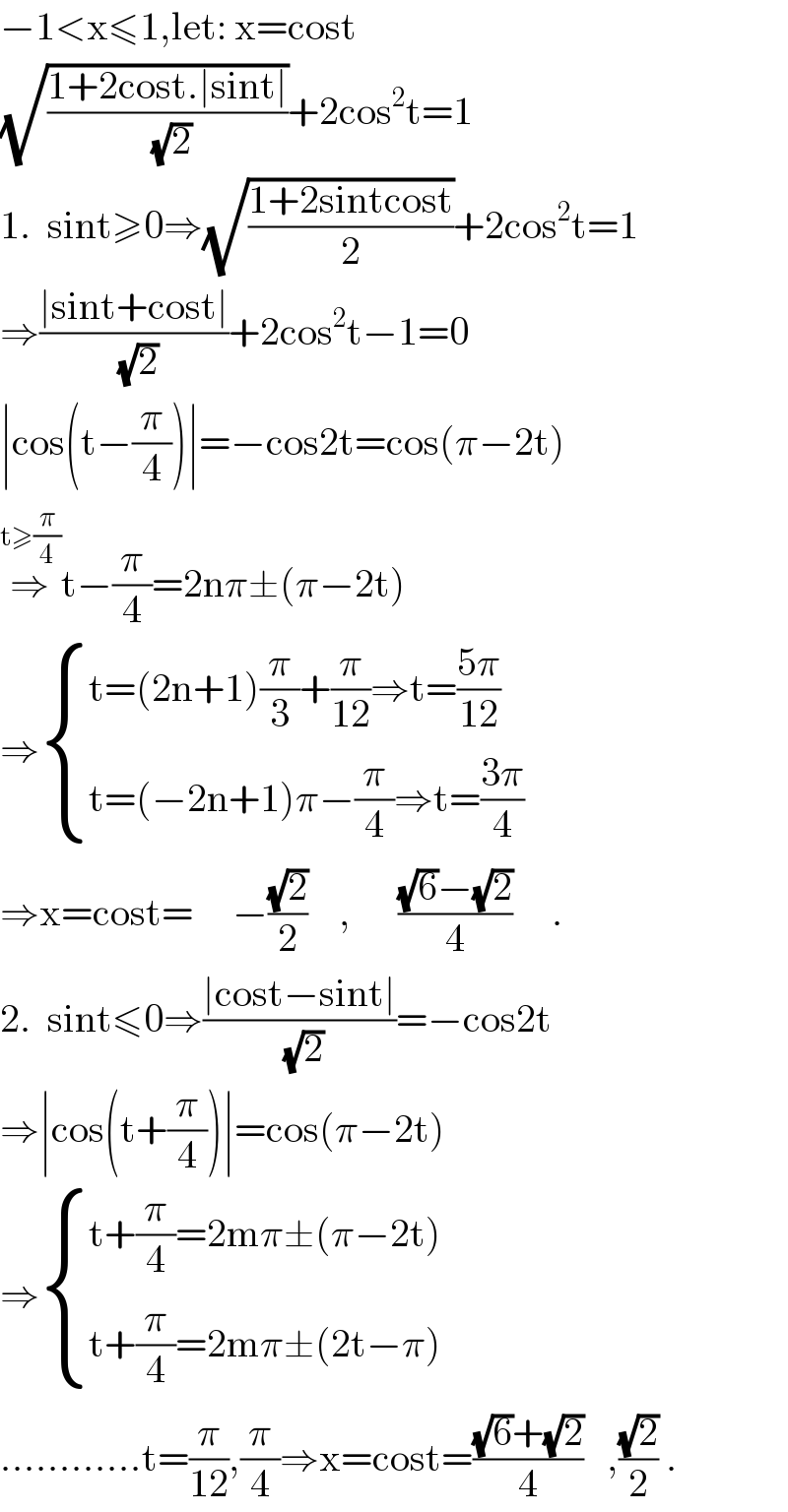
−1<x≤1,let: x=cost (√((1+2cost.∣sint∣)/(√2)))+2cos^2 t=1 1. sint≥0⇒(√((1+2sintcost)/2))+2cos^2 t=1 ⇒((∣sint+cost∣)/(√2))+2cos^2 t−1=0 ∣cos(t−(π/4))∣=−cos2t=cos(π−2t) ⇒^(t≥(π/4)) t−(π/4)=2nπ±(π−2t) ⇒ { ((t=(2n+1)(π/3)+(π/(12))⇒t=((5π)/(12)))),((t=(−2n+1)π−(π/4)⇒t=((3π)/4))) :} ⇒x=cost= −((√2)/2) , (((√6)−(√2))/4) . 2. sint≤0⇒((∣cost−sint∣)/(√2))=−cos2t ⇒∣cos(t+(π/4))∣=cos(π−2t) ⇒ { ((t+(π/4)=2mπ±(π−2t))),((t+(π/4)=2mπ±(2t−π))) :} ............t=(π/(12)),(π/4)⇒x=cost=(((√6)+(√2))/4) ,((√2)/2) .

$$−\mathrm{1}<\mathrm{x}\leqslant\mathrm{1},\mathrm{let}:\:\mathrm{x}=\mathrm{cost} \\ $$$$\sqrt{\frac{\mathrm{1}+\mathrm{2cost}.\mid\mathrm{sint}\mid}{\sqrt{\mathrm{2}}}}+\mathrm{2cos}^{\mathrm{2}} \mathrm{t}=\mathrm{1} \\ $$$$\mathrm{1}.\:\:\mathrm{sint}\geqslant\mathrm{0}\Rightarrow\sqrt{\frac{\mathrm{1}+\mathrm{2sintcost}}{\mathrm{2}}}+\mathrm{2cos}^{\mathrm{2}} \mathrm{t}=\mathrm{1} \\ $$$$\Rightarrow\frac{\mid\mathrm{sint}+\mathrm{cost}\mid}{\sqrt{\mathrm{2}}}+\mathrm{2cos}^{\mathrm{2}} \mathrm{t}−\mathrm{1}=\mathrm{0} \\ $$$$\mid\mathrm{cos}\left(\mathrm{t}−\frac{\pi}{\mathrm{4}}\right)\mid=−\mathrm{cos2t}=\mathrm{cos}\left(\pi−\mathrm{2t}\right) \\ $$$$\overset{\mathrm{t}\geqslant\frac{\pi}{\mathrm{4}}} {\Rightarrow}\mathrm{t}−\frac{\pi}{\mathrm{4}}=\mathrm{2n}\pi\pm\left(\pi−\mathrm{2t}\right) \\ $$$$\Rightarrow\begin{cases}{\mathrm{t}=\left(\mathrm{2n}+\mathrm{1}\right)\frac{\pi}{\mathrm{3}}+\frac{\pi}{\mathrm{12}}\Rightarrow\mathrm{t}=\frac{\mathrm{5}\pi}{\mathrm{12}}}\\{\mathrm{t}=\left(−\mathrm{2n}+\mathrm{1}\right)\pi−\frac{\pi}{\mathrm{4}}\Rightarrow\mathrm{t}=\frac{\mathrm{3}\pi}{\mathrm{4}}}\end{cases} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{cost}=\:\:\:\:\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:\:\:,\:\:\:\:\:\:\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}\:\:\:\:\:. \\ $$$$\mathrm{2}.\:\:\mathrm{sint}\leqslant\mathrm{0}\Rightarrow\frac{\mid\mathrm{cost}−\mathrm{sint}\mid}{\sqrt{\mathrm{2}}}=−\mathrm{cos2t} \\ $$$$\Rightarrow\mid\mathrm{cos}\left(\mathrm{t}+\frac{\pi}{\mathrm{4}}\right)\mid=\mathrm{cos}\left(\pi−\mathrm{2t}\right) \\ $$$$\Rightarrow\begin{cases}{\mathrm{t}+\frac{\pi}{\mathrm{4}}=\mathrm{2m}\pi\pm\left(\pi−\mathrm{2t}\right)}\\{\mathrm{t}+\frac{\pi}{\mathrm{4}}=\mathrm{2m}\pi\pm\left(\mathrm{2t}−\pi\right)}\end{cases} \\ $$$$............\mathrm{t}=\frac{\pi}{\mathrm{12}},\frac{\pi}{\mathrm{4}}\Rightarrow\mathrm{x}=\mathrm{cost}=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}\:\:\:,\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:. \\ $$

Commented by MJS last updated on 20/Jul/19

nice method but you have to verify your solutions. not all of them fit the given equation

$$\mathrm{nice}\:\mathrm{method}\:\mathrm{but}\:\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{verify}\:\mathrm{your} \\ $$$$\mathrm{solutions}.\:\mathrm{not}\:\mathrm{all}\:\mathrm{of}\:\mathrm{them}\:\mathrm{fit}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$

Commented by Mikael last updated on 22/Jul/19

God bless you Sir.

$${God}\:{bless}\:{you}\:{Sir}. \\ $$

Answered by MJS last updated on 19/Jul/19

((√(1+2x(√(1−x^2 ))))/(√2))+2x^2 =1 (√(1+2x(√(1−x^2 ))))=(√2)−2(√2)x^2 squaring (will create false solutions!) 1+2x(√(1−x^2 ))=8x^4 −8x^2 +2 2x(√(1−x^2 ))=8x^4 −8x+1 squaring (will create false solutions!) 4x^2 −4x^4 =64x^8 −128x^6 +80x^4 −16x^2 +1 x^8 −2x^6 +((21)/(16))x^4 −(5/(16))x^2 +(1/(64))=0 x=±(√y) y^4 −2y^3 +((21)/(16))y^2 −(5/(16))y+(1/(64))=0 y=z+(1/2) z^4 −(3/(16))z^2 =0 ⇒ z_1 =−((√3)/4) z_2 =0 z_3 =((√3)/4) ⇒ y_1 =(1/2)−((√3)/4) y_2 =(1/2) y_3 =(1/2)+((√3)/4) ⇒ x_1 =(((√2)−(√6))/4) x_2 =−((√2)/2) x_3 =−(((√2)+(√6))/4) x_4 =(((√6)−(√2))/4) x_5 =((√2)/2) x_6 =(((√2)+(√6))/4) but only x_2 and x_4 solve the given equation x=−((√2)/2)∨x=(((√6)−(√2))/4)

$$\frac{\sqrt{\mathrm{1}+\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}{\sqrt{\mathrm{2}}}+\mathrm{2}{x}^{\mathrm{2}} =\mathrm{1} \\ $$$$\sqrt{\mathrm{1}+\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\mathrm{2}}{x}^{\mathrm{2}} \\ $$$$\mathrm{squaring}\:\left(\mathrm{will}\:\mathrm{create}\:\mathrm{false}\:\mathrm{solutions}!\right) \\ $$$$\mathrm{1}+\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{8}{x}^{\mathrm{4}} −\mathrm{8}{x}^{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{2}{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{8}{x}^{\mathrm{4}} −\mathrm{8}{x}+\mathrm{1} \\ $$$$\mathrm{squaring}\:\left(\mathrm{will}\:\mathrm{create}\:\mathrm{false}\:\mathrm{solutions}!\right) \\ $$$$\mathrm{4}{x}^{\mathrm{2}} −\mathrm{4}{x}^{\mathrm{4}} =\mathrm{64}{x}^{\mathrm{8}} −\mathrm{128}{x}^{\mathrm{6}} +\mathrm{80}{x}^{\mathrm{4}} −\mathrm{16}{x}^{\mathrm{2}} +\mathrm{1} \\ $$$${x}^{\mathrm{8}} −\mathrm{2}{x}^{\mathrm{6}} +\frac{\mathrm{21}}{\mathrm{16}}{x}^{\mathrm{4}} −\frac{\mathrm{5}}{\mathrm{16}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{64}}=\mathrm{0} \\ $$$${x}=\pm\sqrt{{y}} \\ $$$${y}^{\mathrm{4}} −\mathrm{2}{y}^{\mathrm{3}} +\frac{\mathrm{21}}{\mathrm{16}}{y}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{16}}{y}+\frac{\mathrm{1}}{\mathrm{64}}=\mathrm{0} \\ $$$${y}={z}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${z}^{\mathrm{4}} −\frac{\mathrm{3}}{\mathrm{16}}{z}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:{z}_{\mathrm{1}} =−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\:\:{z}_{\mathrm{2}} =\mathrm{0}\:\:{z}_{\mathrm{3}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\Rightarrow\:{y}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\:\:{y}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\:\:{y}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} =\frac{\sqrt{\mathrm{2}}−\sqrt{\mathrm{6}}}{\mathrm{4}}\:\:{x}_{\mathrm{2}} =−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:{x}_{\mathrm{3}} =−\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:{x}_{\mathrm{4}} =\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}\:\:{x}_{\mathrm{5}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\:\:{x}_{\mathrm{6}} =\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{6}}}{\mathrm{4}} \\ $$$$\mathrm{but}\:\mathrm{only}\:{x}_{\mathrm{2}} \:\mathrm{and}\:{x}_{\mathrm{4}} \:\mathrm{solve}\:\mathrm{the}\:\mathrm{given}\:\mathrm{equation} \\ $$$${x}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\vee{x}=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$

Commented by Mikael last updated on 22/Jul/19

Nice solution Sir.

$${Nice}\:{solution}\:{Sir}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com