Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 213423 by efronzo1 last updated on 05/Nov/24

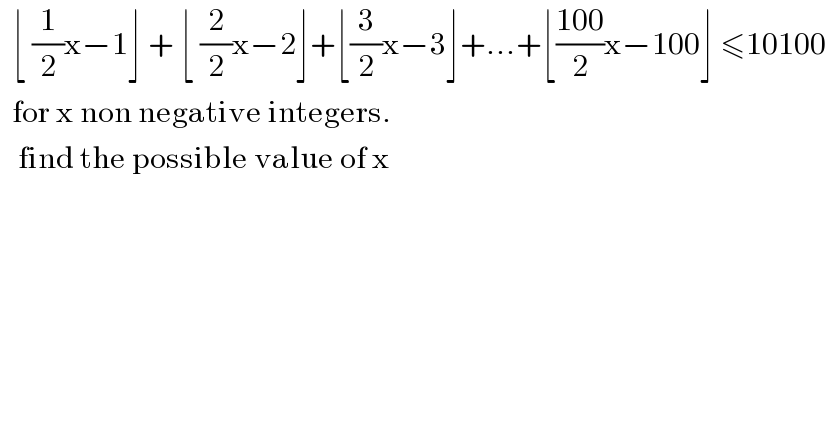
⌊ (1/2)x−1⌋ + ⌊ (2/2)x−2⌋+⌊(3/2)x−3⌋+...+⌊((100)/2)x−100⌋ ≤10100 for x non negative integers. find the possible value of x

$$\:\:\lfloor\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\mathrm{1}\rfloor\:+\:\lfloor\:\frac{\mathrm{2}}{\mathrm{2}}\mathrm{x}−\mathrm{2}\rfloor+\lfloor\frac{\mathrm{3}}{\mathrm{2}}\mathrm{x}−\mathrm{3}\rfloor+...+\lfloor\frac{\mathrm{100}}{\mathrm{2}}\mathrm{x}−\mathrm{100}\rfloor\:\leqslant\mathrm{10100} \\ $$$$\:\:\mathrm{for}\:\mathrm{x}\:\mathrm{non}\:\mathrm{negative}\:\mathrm{integers}. \\ $$$$\:\:\:\mathrm{find}\:\mathrm{the}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x} \\ $$

Answered by golsendro last updated on 05/Nov/24

$$\:\:\:\underline{ } \:\: \\ $$

Commented by hardmath last updated on 05/Nov/24

thankyou dearprofessor

$$\mathrm{thankyou}\:\mathrm{dearprofessor} \\ $$

Commented by mr W last updated on 05/Nov/24

when A≤B is given and you get A≤C, how can you then say C≤B, not B≤C?

$${when}\:{A}\leqslant{B}\:{is}\:{given}\:{and}\:{you}\:{get} \\ $$$${A}\leqslant{C},\:{how}\:{can}\:{you}\:{then}\:{say}\:{C}\leqslant{B}, \\ $$$${not}\:{B}\leqslant{C}? \\ $$

Commented by mr W last updated on 06/Nov/24

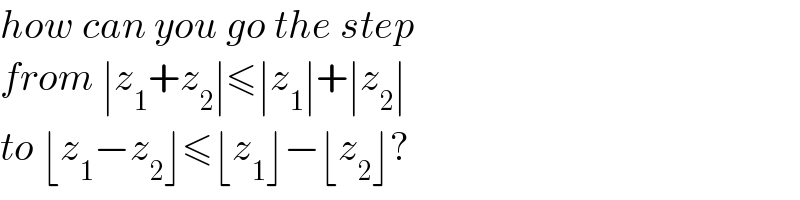
how can you go the step from ∣z_1 +z_2 ∣≤∣z_1 ∣+∣z_2 ∣ to ⌊z_1 −z_2 ⌋≤⌊z_1 ⌋−⌊z_2 ⌋?

$${how}\:{can}\:{you}\:{go}\:{the}\:{step}\: \\ $$$${from}\:\mid{z}_{\mathrm{1}} +{z}_{\mathrm{2}} \mid\leqslant\mid{z}_{\mathrm{1}} \mid+\mid{z}_{\mathrm{2}} \mid \\ $$$${to}\:\lfloor{z}_{\mathrm{1}} −{z}_{\mathrm{2}} \rfloor\leqslant\lfloor{z}_{\mathrm{1}} \rfloor−\lfloor{z}_{\mathrm{2}} \rfloor? \\ $$

Commented by golsendro last updated on 06/Nov/24

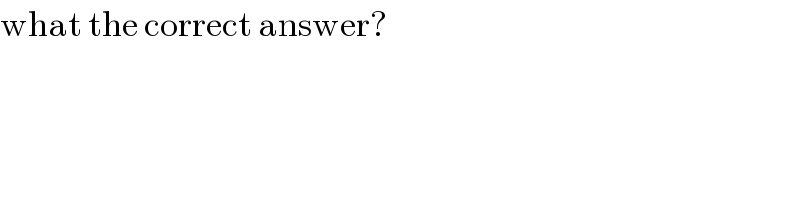
what the correct answer?

$$\mathrm{what}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer}? \\ $$

Commented by mr W last updated on 06/Nov/24

your answer is by accident correct, but your path is wrong.

$${your}\:{answer}\:{is}\:{by}\:{accident}\:{correct}, \\ $$$${but}\:{your}\:{path}\:{is}\:{wrong}. \\ $$

Commented by golsendro last updated on 06/Nov/24

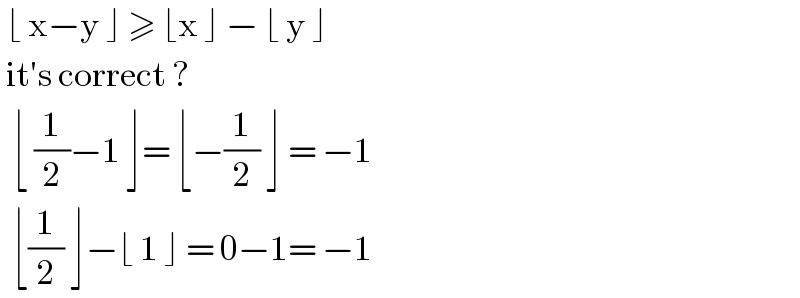
⌊ x−y ⌋ ≥ ⌊x ⌋ − ⌊ y ⌋ it′s correct ? ⌊ (1/2)−1 ⌋= ⌊−(1/2) ⌋ = −1 ⌊(1/2) ⌋−⌊ 1 ⌋ = 0−1= −1

$$\:\lfloor\:\mathrm{x}−\mathrm{y}\:\rfloor\:\geqslant\:\lfloor\mathrm{x}\:\rfloor\:−\:\lfloor\:\mathrm{y}\:\rfloor\: \\ $$$$\:\mathrm{it}'\mathrm{s}\:\mathrm{correct}\:? \\ $$$$\:\:\lfloor\:\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\:\rfloor=\:\lfloor−\frac{\mathrm{1}}{\mathrm{2}}\:\rfloor\:=\:−\mathrm{1} \\ $$$$\:\:\lfloor\frac{\mathrm{1}}{\mathrm{2}}\:\rfloor−\lfloor\:\mathrm{1}\:\rfloor\:=\:\mathrm{0}−\mathrm{1}=\:−\mathrm{1}\: \\ $$

Answered by mr W last updated on 06/Nov/24

case 1: x=even=2n with n≥0 ⌊n−1⌋+⌊2n−2⌋+...+⌊100n−100]≤10100 (1+2+...+100)(n−1)≤10100 5050(n−1)≤10100 ⇒n≤((10100)/(5050))+1=3 ⇒x=0, 2, 4, 6 case 2: x=odd=2n+1 with n≥0 ⌊n+(1/2)−1⌋+⌊2n+1−2⌋+⌊3n+(3/2)−3⌋+...+⌊100n+50−100]≤10100 (1+2+...+100)(n−1)+⌊(1/2)⌋+⌊1⌋+⌊(3/2)⌋+...+⌊((99)/2)⌋+⌊50]≤10100 5050(n−1)+0+2×1+2×2+...+2×49+50≤10100 5050(n−1)+0+2(1+2+...+49+50)−50≤10100 5050(n−1)+50×51−50≤10100 5050(n−1)+2500≤10100 ⇒n≤((10100−2500)/(5050))+1≈2.505 ⇒n=0, 1, 2 ⇒x=1, 3, 5 summary: x=0, 1, 2, 3, 4, 5, 6

$$\boldsymbol{{case}}\:\mathrm{1}:\:{x}={even}=\mathrm{2}{n}\:{with}\:{n}\geqslant\mathrm{0} \\ $$$$\left.\lfloor{n}−\mathrm{1}\rfloor+\lfloor\mathrm{2}{n}−\mathrm{2}\rfloor+...+\lfloor\mathrm{100}{n}−\mathrm{100}\right]\leqslant\mathrm{10100} \\ $$$$\left(\mathrm{1}+\mathrm{2}+...+\mathrm{100}\right)\left({n}−\mathrm{1}\right)\leqslant\mathrm{10100} \\ $$$$\mathrm{5050}\left({n}−\mathrm{1}\right)\leqslant\mathrm{10100} \\ $$$$\Rightarrow{n}\leqslant\frac{\mathrm{10100}}{\mathrm{5050}}+\mathrm{1}=\mathrm{3}\: \\ $$$$\Rightarrow{x}=\mathrm{0},\:\mathrm{2},\:\mathrm{4},\:\mathrm{6} \\ $$$$\boldsymbol{{case}}\:\mathrm{2}:\:{x}={odd}=\mathrm{2}{n}+\mathrm{1}\:{with}\:{n}\geqslant\mathrm{0} \\ $$$$\left.\lfloor{n}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}\rfloor+\lfloor\mathrm{2}{n}+\mathrm{1}−\mathrm{2}\rfloor+\lfloor\mathrm{3}{n}+\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{3}\rfloor+...+\lfloor\mathrm{100}{n}+\mathrm{50}−\mathrm{100}\right]\leqslant\mathrm{10100} \\ $$$$\left.\left(\mathrm{1}+\mathrm{2}+...+\mathrm{100}\right)\left({n}−\mathrm{1}\right)+\lfloor\frac{\mathrm{1}}{\mathrm{2}}\rfloor+\lfloor\mathrm{1}\rfloor+\lfloor\frac{\mathrm{3}}{\mathrm{2}}\rfloor+...+\lfloor\frac{\mathrm{99}}{\mathrm{2}}\rfloor+\lfloor\mathrm{50}\right]\leqslant\mathrm{10100} \\ $$$$\mathrm{5050}\left({n}−\mathrm{1}\right)+\mathrm{0}+\mathrm{2}×\mathrm{1}+\mathrm{2}×\mathrm{2}+...+\mathrm{2}×\mathrm{49}+\mathrm{50}\leqslant\mathrm{10100} \\ $$$$\mathrm{5050}\left({n}−\mathrm{1}\right)+\mathrm{0}+\mathrm{2}\left(\mathrm{1}+\mathrm{2}+...+\mathrm{49}+\mathrm{50}\right)−\mathrm{50}\leqslant\mathrm{10100} \\ $$$$\mathrm{5050}\left({n}−\mathrm{1}\right)+\mathrm{50}×\mathrm{51}−\mathrm{50}\leqslant\mathrm{10100} \\ $$$$\mathrm{5050}\left({n}−\mathrm{1}\right)+\mathrm{2500}\leqslant\mathrm{10100} \\ $$$$\Rightarrow{n}\leqslant\frac{\mathrm{10100}−\mathrm{2500}}{\mathrm{5050}}+\mathrm{1}\approx\mathrm{2}.\mathrm{505}\:\Rightarrow{n}=\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$$$\Rightarrow{x}=\mathrm{1},\:\mathrm{3},\:\mathrm{5} \\ $$$${summary}: \\ $$$${x}=\mathrm{0},\:\mathrm{1},\:\mathrm{2},\:\mathrm{3},\:\mathrm{4},\:\mathrm{5},\:\mathrm{6} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com