
Question Number 130555 by Dwaipayan Shikari last updated on 26/Jan/21
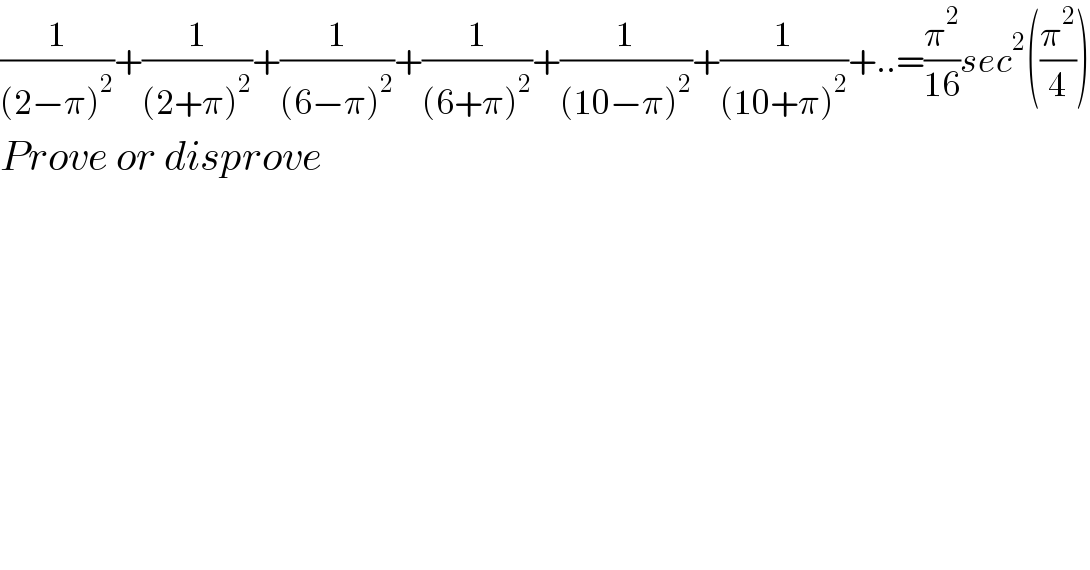
$$\frac{\mathrm{1}}{\left(\mathrm{2}−\pi\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}+\pi\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{6}−\pi\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{6}+\pi\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{10}−\pi\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{10}+\pi\right)^{\mathrm{2}} }+..=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}{sec}^{\mathrm{2}} \left(\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$${Prove}\:{or}\:{disprove} \\ $$
Answered by mindispower last updated on 27/Jan/21

$${S}=\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{4}{k}+\mathrm{2}−\pi\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{4}{k}+\mathrm{2}+\pi\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{16}}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left({k}+\frac{\mathrm{2}−\pi}{\mathrm{4}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({k}+\frac{\mathrm{2}+\pi}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$${cot}\left({x}\right)=\frac{\mathrm{1}}{{x}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left({x}−\pi{n}\right)}+\frac{\mathrm{1}}{\left({x}+\pi{n}\right)} \\ $$$$\Rightarrow{tg}\left(\pi{x}\right)={cot}\left(\frac{\pi}{\mathrm{2}}−{x}\right)=\frac{\mathrm{2}}{\pi−\mathrm{2}{x}}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{2}}{\pi−\mathrm{2}{x}−\mathrm{2}\pi{n}}+\frac{\mathrm{2}}{\pi−\mathrm{2}{x}+\mathrm{2}\pi{n}} \\ $$$$\Rightarrow\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)=\frac{\mathrm{4}}{\left(\pi−\mathrm{2}{x}\right)^{\mathrm{2}} }+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{4}}{\left(\pi−\mathrm{2}{x}−\mathrm{2}\pi{n}\right)^{\mathrm{2}} }+\frac{\mathrm{4}}{\left(\pi−\mathrm{2}{x}+\mathrm{2}\pi{n}\right)^{\mathrm{2}} }={H} \\ $$$${x}=\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Rightarrow{H}=\frac{\mathrm{4}}{\left(\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} }+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{4}}{\left(\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}\pi{n}\right)}+\frac{\mathrm{4}}{\left(\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\pi{n}\right)^{\mathrm{2}} }={A}+{B} \\ $$$${B}=\underset{{n}\geqslant\mathrm{0}} {\sum}\left\{\frac{\mathrm{4}}{\left(−\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\mathrm{2}{n}\pi\right)^{\mathrm{2}} }+\frac{\mathrm{4}}{\left(\pi+\mathrm{2}\pi{n}−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} }\right\}−\frac{\mathrm{4}}{\left(\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\pi^{\mathrm{2}} }\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\frac{\mathrm{2}+\pi}{\mathrm{4}}+{n}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\frac{\mathrm{2}−\pi}{\mathrm{4}}\right)^{\mathrm{2}} }−\frac{\mathrm{4}}{\left(\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{16}}{\pi^{\mathrm{2}} }{S}−\frac{\mathrm{4}}{\left(\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} }={sec}^{\mathrm{2}} \left(\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\right)−\frac{\mathrm{4}}{\left(\pi−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{S}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}{sec}^{\mathrm{2}} \left(\frac{\pi^{\mathrm{2}} }{\mathrm{4}}\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 27/Jan/21
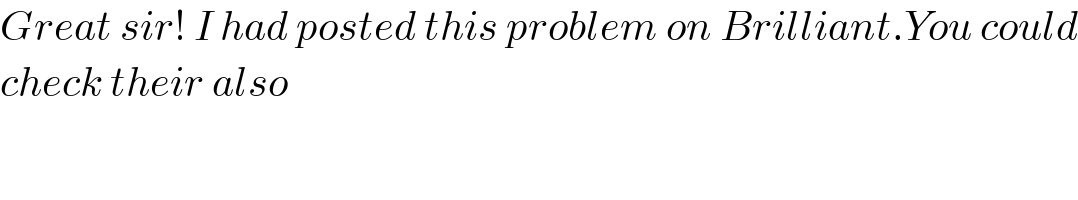
$${Great}\:{sir}!\:{I}\:{had}\:{posted}\:{this}\:{problem}\:{on}\:{Brilliant}.{You}\:{could} \\ $$$${check}\:{their}\:{also} \\ $$
Commented by mindispower last updated on 27/Jan/21
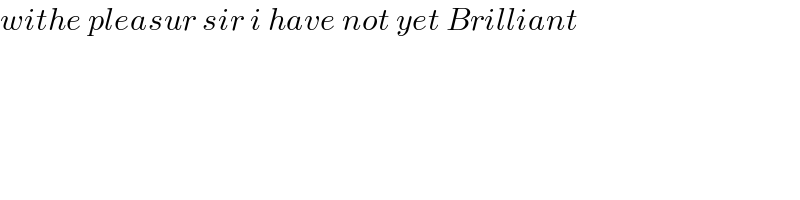
$${withe}\:{pleasur}\:{sir}\:{i}\:{have}\:{not}\:{yet}\:{Brilliant} \\ $$$$ \\ $$
