Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 167419 by Bagus1003 last updated on 16/Mar/22

((1/2))!=? Use Method and Formula!!!!!!!!!

$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!=? \\ $$$${Use}\:{Method}\:{and}\:{Formula}!!!!!!!!! \\ $$

Commented by mkam last updated on 16/Mar/22

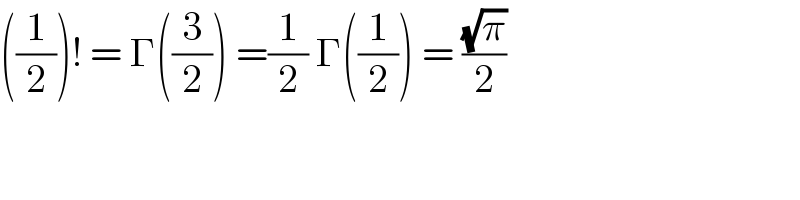
((1/2))! = Γ((3/2)) =(1/2) Γ((1/2)) = ((√π)/2)

$$\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!\:=\:\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\mathrm{1}}{\mathrm{2}}\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$

Answered by alephzero last updated on 16/Mar/22

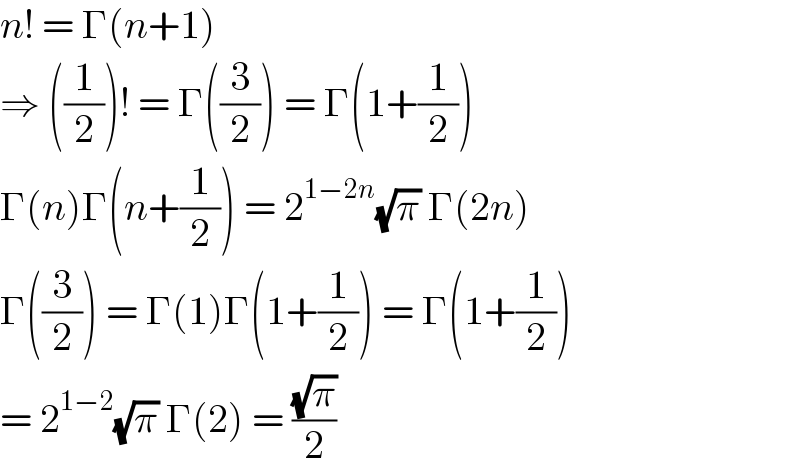
n! = Γ(n+1) ⇒ ((1/2))! = Γ((3/2)) = Γ(1+(1/2)) Γ(n)Γ(n+(1/2)) = 2^(1−2n) (√π) Γ(2n) Γ((3/2)) = Γ(1)Γ(1+(1/2)) = Γ(1+(1/2)) = 2^(1−2) (√π) Γ(2) = ((√π)/2)

$${n}!\:=\:\Gamma\left({n}+\mathrm{1}\right) \\ $$$$\Rightarrow\:\left(\frac{\mathrm{1}}{\mathrm{2}}\right)!\:=\:\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\:\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\Gamma\left({n}\right)\Gamma\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\mathrm{2}^{\mathrm{1}−\mathrm{2}{n}} \sqrt{\pi}\:\Gamma\left(\mathrm{2}{n}\right) \\ $$$$\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\:\Gamma\left(\mathrm{1}\right)\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\:\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\:\mathrm{2}^{\mathrm{1}−\mathrm{2}} \sqrt{\pi}\:\Gamma\left(\mathrm{2}\right)\:=\:\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com