Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 202780 by BaliramKumar last updated on 03/Jan/24

1+2+4+7+11+16+............up to 25 terms = ?

$$\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{7}+\mathrm{11}+\mathrm{16}+............\mathrm{up}\:\mathrm{to}\:\mathrm{25}\:\mathrm{terms}\:=\:? \\ $$

Answered by mr W last updated on 03/Jan/24

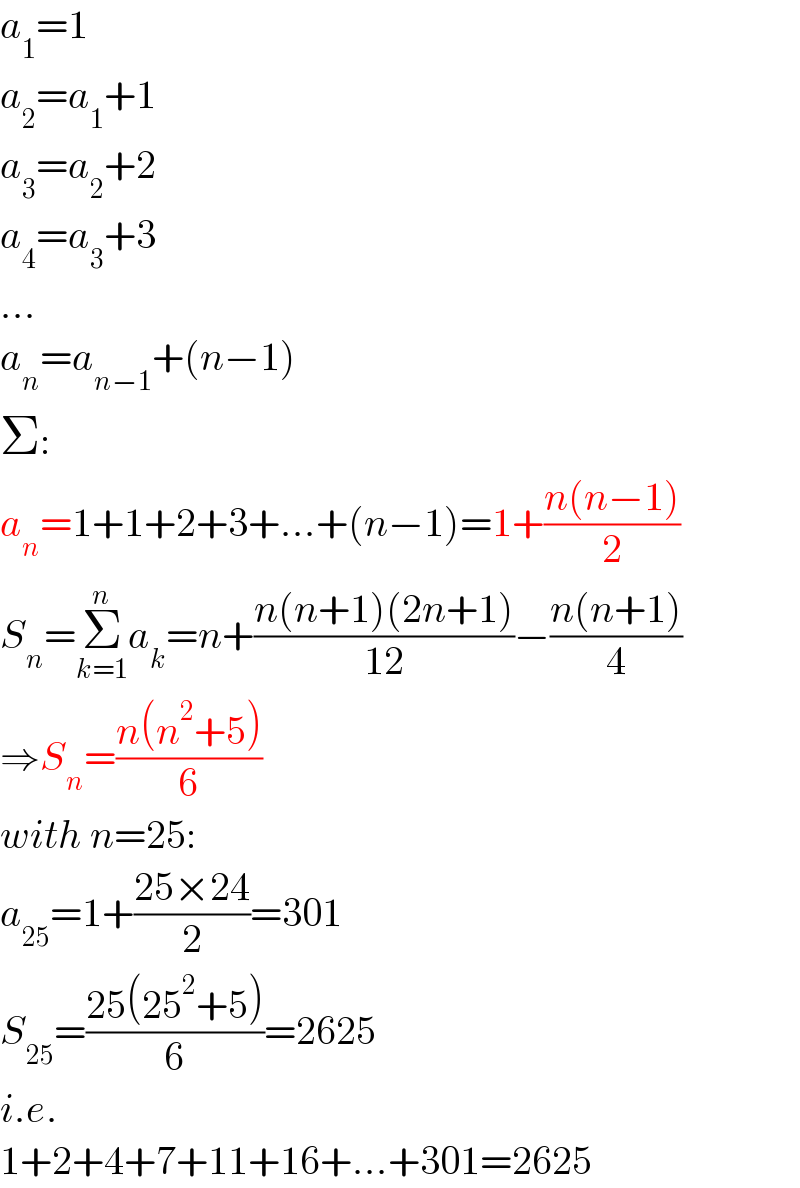
a_1 =1 a_2 =a_1 +1 a_3 =a_2 +2 a_4 =a_3 +3 ... a_n =a_(n−1) +(n−1) Σ: a_n =1+1+2+3+...+(n−1)=1+((n(n−1))/2) S_n =Σ_(k=1) ^n a_k =n+((n(n+1)(2n+1))/(12))−((n(n+1))/4) ⇒S_n =((n(n^2 +5))/6) with n=25: a_(25) =1+((25×24)/2)=301 S_(25) =((25(25^2 +5))/6)=2625 i.e. 1+2+4+7+11+16+...+301=2625

$${a}_{\mathrm{1}} =\mathrm{1} \\ $$$${a}_{\mathrm{2}} ={a}_{\mathrm{1}} +\mathrm{1} \\ $$$${a}_{\mathrm{3}} ={a}_{\mathrm{2}} +\mathrm{2} \\ $$$${a}_{\mathrm{4}} ={a}_{\mathrm{3}} +\mathrm{3} \\ $$$$... \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{1}} +\left({n}−\mathrm{1}\right) \\ $$$$\Sigma: \\ $$$${a}_{{n}} =\mathrm{1}+\mathrm{1}+\mathrm{2}+\mathrm{3}+...+\left({n}−\mathrm{1}\right)=\mathrm{1}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$${S}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{k}} ={n}+\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}}−\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{4}} \\ $$$$\Rightarrow{S}_{{n}} =\frac{{n}\left({n}^{\mathrm{2}} +\mathrm{5}\right)}{\mathrm{6}} \\ $$$${with}\:{n}=\mathrm{25}: \\ $$$${a}_{\mathrm{25}} =\mathrm{1}+\frac{\mathrm{25}×\mathrm{24}}{\mathrm{2}}=\mathrm{301} \\ $$$${S}_{\mathrm{25}} =\frac{\mathrm{25}\left(\mathrm{25}^{\mathrm{2}} +\mathrm{5}\right)}{\mathrm{6}}=\mathrm{2625} \\ $$$${i}.{e}. \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{7}+\mathrm{11}+\mathrm{16}+...+\mathrm{301}=\mathrm{2625} \\ $$

Commented by BaliramKumar last updated on 03/Jan/24

Thanks Sir

$$\mathrm{Thanks}\:\mathrm{Sir} \\ $$

Answered by talminator2856792 last updated on 03/Jan/24

1+2+3+4+...+n = ((n(n+1))/2) 1+3+6+10+...+ ((n(n+1))/2) = ((n(n+1)(n+2))/6) 1+2+4+7+11+...+a_n = (1+2+3+4+5+...+n) + (0+0+1+3+6+...+ (((n−1)(n−2))/2)) = ((n(n+1))/2) + ((n(n−1)(n−2))/6) → 1+2+4+7+11+16+...+a_(25) = 325+ 2300 = 2625

$$\:\:\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+...+{n} \\ $$$$\:\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\:\: \\ $$$$\:\:\mathrm{1}+\mathrm{3}+\mathrm{6}+\mathrm{10}+...+\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\:\:=\:\frac{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}{\mathrm{6}} \\ $$$$\:\: \\ $$$$\:\:\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{7}+\mathrm{11}+...+{a}_{{n}} \\ $$$$\:\:=\:\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+...+{n}\right)\:+ \\ $$$$\:\:\:\:\:\:\:\left(\mathrm{0}+\mathrm{0}+\mathrm{1}+\mathrm{3}+\mathrm{6}+...+\:\frac{\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{2}}\right) \\ $$$$\:\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}\:+\:\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{6}} \\ $$$$\:\: \\ $$$$\:\:\rightarrow\:\mathrm{1}+\mathrm{2}+\mathrm{4}+\mathrm{7}+\mathrm{11}+\mathrm{16}+...+{a}_{\mathrm{25}} \\ $$$$\:\:=\:\mathrm{325}+\:\mathrm{2300} \\ $$$$\:\:=\:\mathrm{2625} \\ $$

Commented by BaliramKumar last updated on 03/Jan/24

Thanks Sir

$$\mathrm{Thanks}\:\mathrm{Sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com