Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 158088 by Gbenga last updated on 31/Oct/21

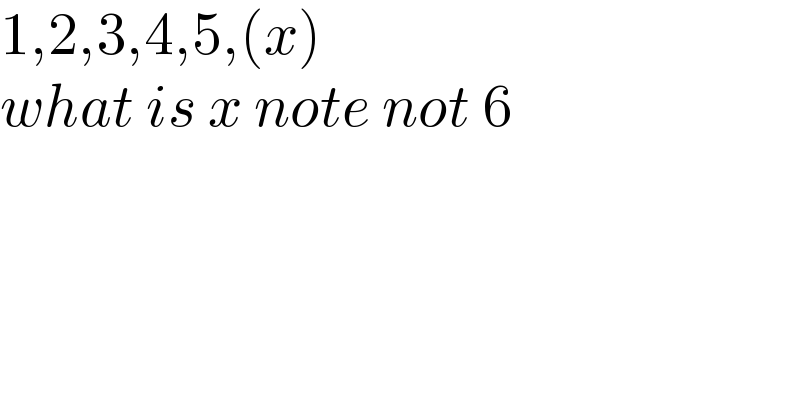
1,2,3,4,5,(x) what is x note not 6

$$\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\left({x}\right) \\ $$$${what}\:{is}\:{x}\:{note}\:{not}\:\mathrm{6} \\ $$

Commented by MJS_new last updated on 31/Oct/21

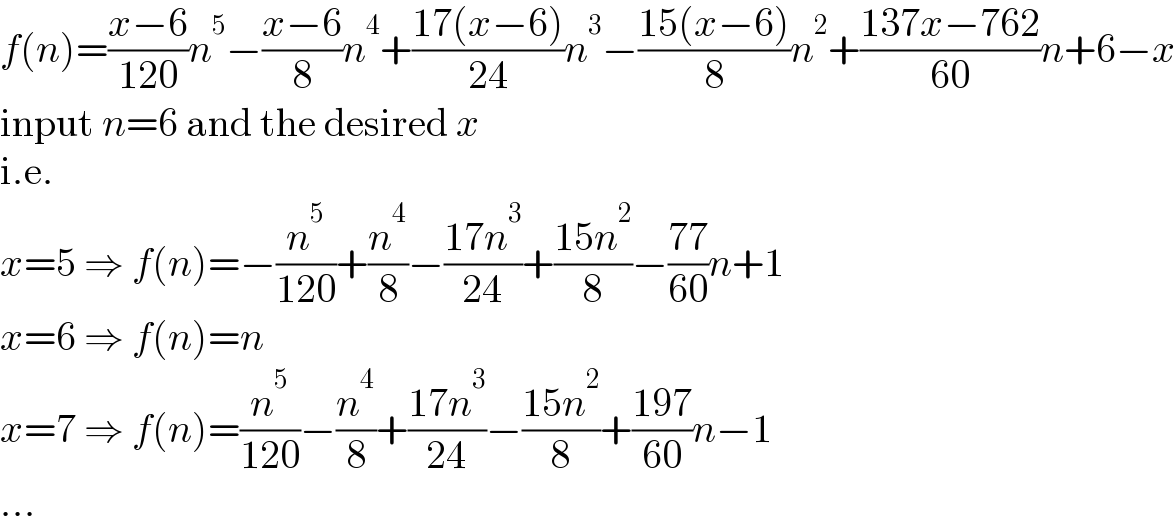
f(n)=((x−6)/(120))n^5 −((x−6)/8)n^4 +((17(x−6))/(24))n^3 −((15(x−6))/8)n^2 +((137x−762)/(60))n+6−x input n=6 and the desired x i.e. x=5 ⇒ f(n)=−(n^5 /(120))+(n^4 /8)−((17n^3 )/(24))+((15n^2 )/8)−((77)/(60))n+1 x=6 ⇒ f(n)=n x=7 ⇒ f(n)=(n^5 /(120))−(n^4 /8)+((17n^3 )/(24))−((15n^2 )/8)+((197)/(60))n−1 ...

$${f}\left({n}\right)=\frac{{x}−\mathrm{6}}{\mathrm{120}}{n}^{\mathrm{5}} −\frac{{x}−\mathrm{6}}{\mathrm{8}}{n}^{\mathrm{4}} +\frac{\mathrm{17}\left({x}−\mathrm{6}\right)}{\mathrm{24}}{n}^{\mathrm{3}} −\frac{\mathrm{15}\left({x}−\mathrm{6}\right)}{\mathrm{8}}{n}^{\mathrm{2}} +\frac{\mathrm{137}{x}−\mathrm{762}}{\mathrm{60}}{n}+\mathrm{6}−{x} \\ $$$$\mathrm{input}\:{n}=\mathrm{6}\:\mathrm{and}\:\mathrm{the}\:\mathrm{desired}\:{x} \\ $$$$\mathrm{i}.\mathrm{e}. \\ $$$${x}=\mathrm{5}\:\Rightarrow\:{f}\left({n}\right)=−\frac{{n}^{\mathrm{5}} }{\mathrm{120}}+\frac{{n}^{\mathrm{4}} }{\mathrm{8}}−\frac{\mathrm{17}{n}^{\mathrm{3}} }{\mathrm{24}}+\frac{\mathrm{15}{n}^{\mathrm{2}} }{\mathrm{8}}−\frac{\mathrm{77}}{\mathrm{60}}{n}+\mathrm{1} \\ $$$${x}=\mathrm{6}\:\Rightarrow\:{f}\left({n}\right)={n} \\ $$$${x}=\mathrm{7}\:\Rightarrow\:{f}\left({n}\right)=\frac{{n}^{\mathrm{5}} }{\mathrm{120}}−\frac{{n}^{\mathrm{4}} }{\mathrm{8}}+\frac{\mathrm{17}{n}^{\mathrm{3}} }{\mathrm{24}}−\frac{\mathrm{15}{n}^{\mathrm{2}} }{\mathrm{8}}+\frac{\mathrm{197}}{\mathrm{60}}{n}−\mathrm{1} \\ $$$$... \\ $$

Answered by MJS_new last updated on 31/Oct/21

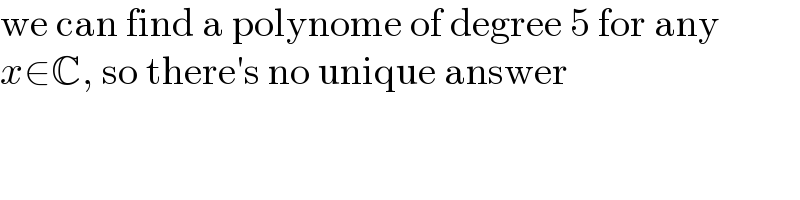
we can find a polynome of degree 5 for any x∈C, so there′s no unique answer

$$\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{a}\:\mathrm{polynome}\:\mathrm{of}\:\mathrm{degree}\:\mathrm{5}\:\mathrm{for}\:\mathrm{any} \\ $$$${x}\in\mathbb{C},\:\mathrm{so}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{unique}\:\mathrm{answer} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com