
Question Number 108609 by Rio Michael last updated on 18/Aug/20
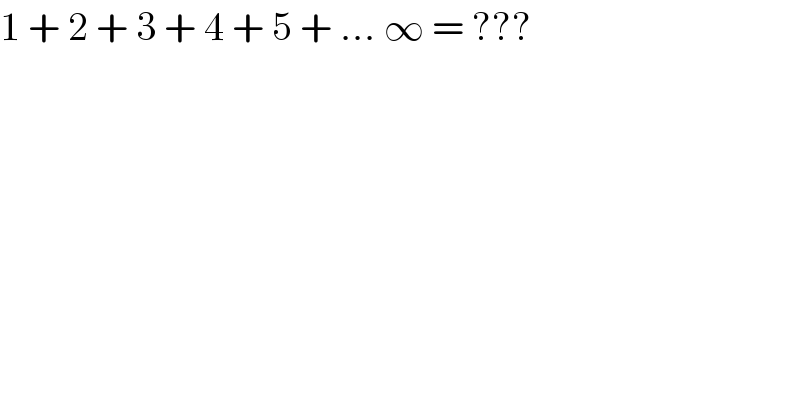
$$\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{3}\:+\:\mathrm{4}\:+\:\mathrm{5}\:+\:...\:\infty\:=\:??? \\ $$
Commented by ajfour last updated on 18/Aug/20

$${S}_{{n}} =\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$
Answered by Dwaipayan Shikari last updated on 18/Aug/20

$${S}=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+.... \\ $$$$\mathrm{4}{S}=\:\:\:\:\mathrm{4}\:\:\:\:+\:\:\:\:\mathrm{8}\:\:\:+\:\:\:\:\mathrm{12}\: \\ $$$$−\mathrm{3}{S}=\mathrm{1}−\mathrm{2}+\mathrm{3}−\mathrm{4}+\mathrm{5}−\mathrm{6}+.... \\ $$$$−\mathrm{3}{S}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${S}=−\frac{\mathrm{1}}{\mathrm{12}} \\ $$$$\circledast \\ $$$${S}=\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{6}+\mathrm{7}+\mathrm{8}+\mathrm{9}+... \\ $$$${S}=\:\mathrm{1}+\left(\mathrm{2}+\mathrm{3}+\mathrm{4}\right)+\left(\mathrm{5}+\mathrm{6}+\mathrm{7}\right)+\left(\mathrm{8}+\mathrm{9}+\mathrm{10}\right)+... \\ $$$${S}=\mathrm{1}+\mathrm{9}+\mathrm{18}+\mathrm{27}+.... \\ $$$${S}=\mathrm{1}+\mathrm{9}\left(\mathrm{1}+\mathrm{2}+\mathrm{3}+\mathrm{4}+....\right) \\ $$$${S}=\mathrm{1}+\mathrm{9}{S} \\ $$$${S}=−\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\circledast{S}=\mathrm{1}+\left(\mathrm{1}+\mathrm{1}\right)+\left(\mathrm{1}+\mathrm{1}+\mathrm{1}\right)+.... \\ $$$$\:\:\:\:{S}=\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:+\left(\mathrm{1}+\mathrm{1}\right)+..... \\ $$$$...... \\ $$$${subtracting} \\ $$$$\mathrm{0}=\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+\mathrm{1}+.... \\ $$$$ \\ $$
Commented by Rio Michael last updated on 18/Aug/20
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{sir}. \\ $$
Commented by Dwaipayan Shikari last updated on 18/Aug/20
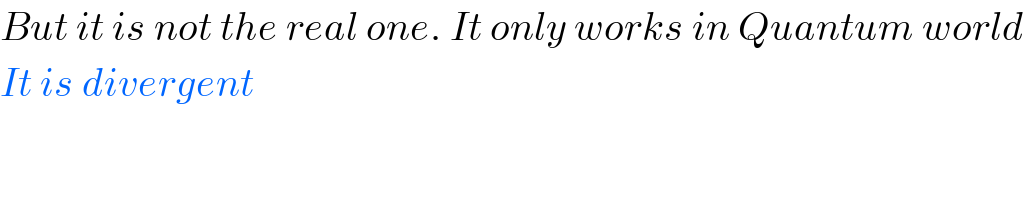
$${But}\:{it}\:{is}\:{not}\:{the}\:{real}\:{one}.\:{It}\:{only}\:{works}\:{in}\:{Quantum}\:{world} \\ $$$${It}\:{is}\:{divergent} \\ $$
