
Question Number 6353 by sanusihammed last updated on 24/Jun/16
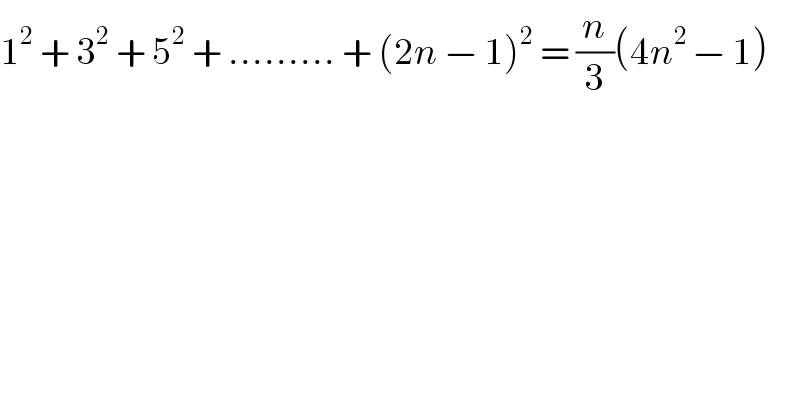
$$\mathrm{1}^{\mathrm{2}} \:+\:\mathrm{3}^{\mathrm{2}} \:+\:\mathrm{5}^{\mathrm{2}} \:+\:.........\:+\:\left(\mathrm{2}{n}\:−\:\mathrm{1}\right)^{\mathrm{2}} \:=\:\frac{{n}}{\mathrm{3}}\left(\mathrm{4}{n}^{\mathrm{2}\:} −\:\mathrm{1}\right) \\ $$
Commented by prakash jain last updated on 24/Jun/16
![(k/3)(4k^2 −1)+[2(k+1)−1]^2 =(k/3)(4k^2 −1)+(2k+1)^2 =(1/3)[4k^3 −k+12k^2 +12k+3] =(1/3)[4k^3 +12k^2 +11k+3] =(1/3)[4k^3 +4k^2 +8k^2 +8k+3k+3] =((k+1)/3)[4k^2 +8k+3] =((k+1)/3)[4k^2 +8k+4−1] =((k+1)/3)[4(k+1)^2 −1] ■](Q6362.png)
$$\frac{{k}}{\mathrm{3}}\left(\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}\right)+\left[\mathrm{2}\left({k}+\mathrm{1}\right)−\mathrm{1}\right]^{\mathrm{2}} \\ $$$$=\frac{{k}}{\mathrm{3}}\left(\mathrm{4}{k}^{\mathrm{2}} −\mathrm{1}\right)+\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{4}{k}^{\mathrm{3}} −{k}+\mathrm{12}{k}^{\mathrm{2}} +\mathrm{12}{k}+\mathrm{3}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{4}{k}^{\mathrm{3}} +\mathrm{12}{k}^{\mathrm{2}} +\mathrm{11}{k}+\mathrm{3}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left[\mathrm{4}{k}^{\mathrm{3}} +\mathrm{4}{k}^{\mathrm{2}} +\mathrm{8}{k}^{\mathrm{2}} +\mathrm{8}{k}+\mathrm{3}{k}+\mathrm{3}\right] \\ $$$$=\frac{{k}+\mathrm{1}}{\mathrm{3}}\left[\mathrm{4}{k}^{\mathrm{2}} +\mathrm{8}{k}+\mathrm{3}\right] \\ $$$$=\frac{{k}+\mathrm{1}}{\mathrm{3}}\left[\mathrm{4}{k}^{\mathrm{2}} +\mathrm{8}{k}+\mathrm{4}−\mathrm{1}\right] \\ $$$$=\frac{{k}+\mathrm{1}}{\mathrm{3}}\left[\mathrm{4}\left({k}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right] \\ $$$$\blacksquare \\ $$
Commented by sanusihammed last updated on 25/Jun/16

$${Thanks} \\ $$
