
Question Number 134812 by mohammad17 last updated on 07/Mar/21
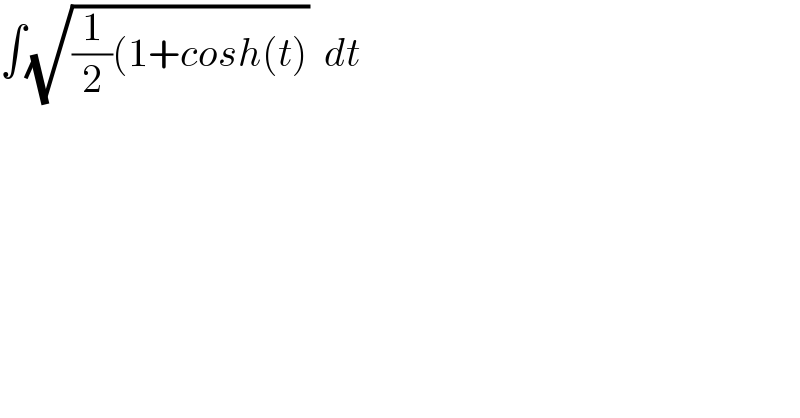
$$\int\sqrt{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+{cosh}\left({t}\right)\right.}\:\:{dt} \\ $$
Answered by mathmax by abdo last updated on 07/Mar/21
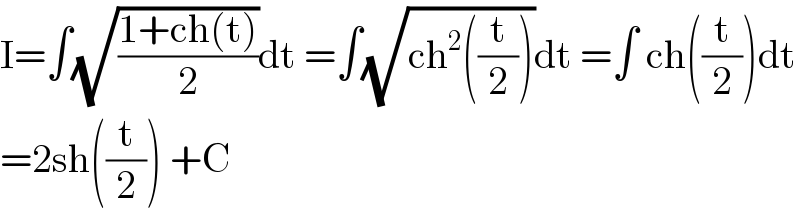
$$\mathrm{I}=\int\sqrt{\frac{\mathrm{1}+\mathrm{ch}\left(\mathrm{t}\right)}{\mathrm{2}}}\mathrm{dt}\:=\int\sqrt{\mathrm{ch}^{\mathrm{2}} \left(\frac{\mathrm{t}}{\mathrm{2}}\right)}\mathrm{dt}\:=\int\:\mathrm{ch}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\mathrm{dt} \\ $$$$=\mathrm{2sh}\left(\frac{\mathrm{t}}{\mathrm{2}}\right)\:+\mathrm{C} \\ $$
