
Question Number 140090 by mathdanisur last updated on 04/May/21
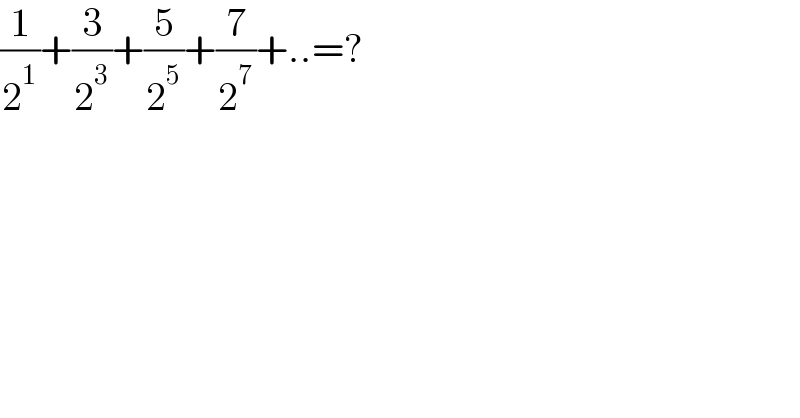
$$\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{5}} }+\frac{\mathrm{7}}{\mathrm{2}^{\mathrm{7}} }+..=? \\ $$
Answered by qaz last updated on 04/May/21
![S=Σ_(n=0) ^∞ ((2n+1)/2^(2n+1) )=Σ_(n=0) ^∞ (1/4^n )(n+(1/2)) =(xD+(1/2))∣_(x=1/4) Σ_(n=0) ^∞ x^n =(xD+(1/2))∣_(x=1/4) (1/(1−x)) =[(x/((1−x)^2 ))+(1/(2(1−x)))]_(x=1/4) =((10)/9)](Q140096.png)
$${S}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{n}+\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}+\mathrm{1}} }=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{4}^{{n}} }\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\left({xD}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mid_{{x}=\mathrm{1}/\mathrm{4}} \underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} =\left({xD}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mid_{{x}=\mathrm{1}/\mathrm{4}} \frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$=\left[\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}−{x}\right)}\right]_{{x}=\mathrm{1}/\mathrm{4}} =\frac{\mathrm{10}}{\mathrm{9}} \\ $$
Commented by mathdanisur last updated on 04/May/21

$${cool}\:{thakyou}\:{sir} \\ $$
Answered by EDWIN88 last updated on 04/May/21
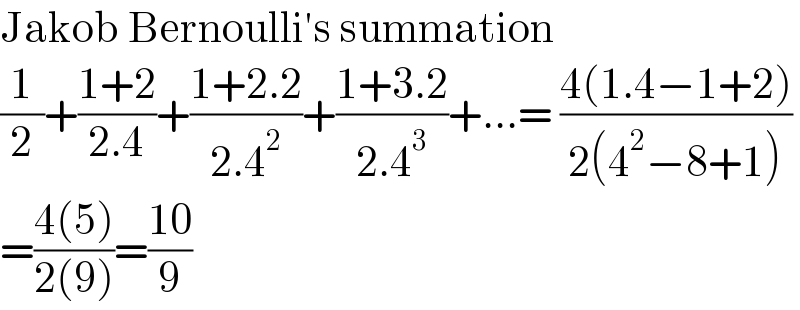
$$\mathrm{Jakob}\:\mathrm{Bernoulli}'\mathrm{s}\:\mathrm{summation}\: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}+\mathrm{2}}{\mathrm{2}.\mathrm{4}}+\frac{\mathrm{1}+\mathrm{2}.\mathrm{2}}{\mathrm{2}.\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{1}+\mathrm{3}.\mathrm{2}}{\mathrm{2}.\mathrm{4}^{\mathrm{3}} }+...=\:\frac{\mathrm{4}\left(\mathrm{1}.\mathrm{4}−\mathrm{1}+\mathrm{2}\right)}{\mathrm{2}\left(\mathrm{4}^{\mathrm{2}} −\mathrm{8}+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{4}\left(\mathrm{5}\right)}{\mathrm{2}\left(\mathrm{9}\right)}=\frac{\mathrm{10}}{\mathrm{9}} \\ $$
Commented by mathdanisur last updated on 04/May/21

$${cool}\:{thanks}\:{sir} \\ $$
