
Question Number 82474 by zainal tanjung last updated on 21/Feb/20
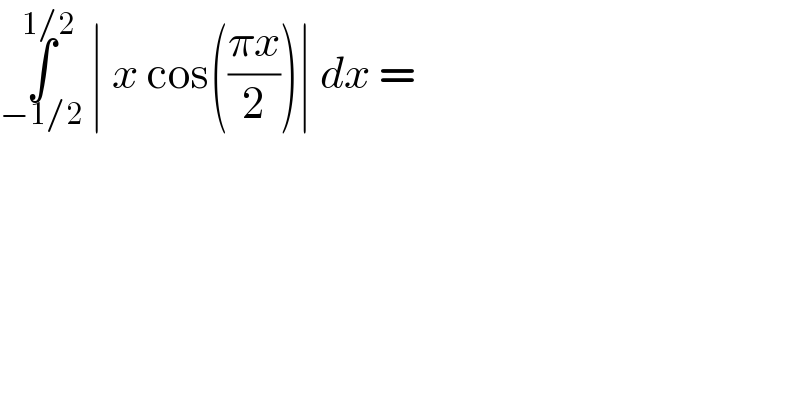
$$\underset{−\mathrm{1}/\mathrm{2}} {\overset{\mathrm{1}/\mathrm{2}} {\int}}\:\mid\:{x}\:\mathrm{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid\:{dx}\:= \\ $$
Commented by mathmax by abdo last updated on 21/Feb/20
![let I =∫_(−(1/2)) ^(1/2) ∣xcos(((πx)/2))∣dx ⇒I =2∫_0 ^(1/2) ∣x∣∣cos(((πx)/2))∣dx changement ((πx)/2) =t give I=2 ∫_0 ^(π/4) (2/π)t cost ×(2/π)dt =(8/π^2 ) ∫_0 ^(π/4) tcost dt =_(by parts) (8/π^2 ){ [tsint]_0 ^(π/4) −∫_0 ^(π/4) sint dt} =(8/π^2 ){(π/(4(√2))) +[cost]_0 ^(π/4) } =(8/π^2 ){(π/(4(√2))) +(1/(√2))−1}](Q82486.png)
$${let}\:{I}\:=\int_{−\frac{\mathrm{1}}{\mathrm{2}}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \mid{xcos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid{dx}\:\Rightarrow{I}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \mid{x}\mid\mid{cos}\left(\frac{\pi{x}}{\mathrm{2}}\right)\mid{dx} \\ $$$${changement}\:\frac{\pi{x}}{\mathrm{2}}\:={t}\:{give}\:{I}=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{2}}{\pi}{t}\:{cost}\:×\frac{\mathrm{2}}{\pi}{dt} \\ $$$$=\frac{\mathrm{8}}{\pi^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{tcost}\:{dt}\:=_{{by}\:{parts}} \:\:\frac{\mathrm{8}}{\pi^{\mathrm{2}} }\left\{\:\:\left[{tsint}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:{sint}\:{dt}\right\} \\ $$$$=\frac{\mathrm{8}}{\pi^{\mathrm{2}} }\left\{\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:+\left[{cost}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \right\}\:=\frac{\mathrm{8}}{\pi^{\mathrm{2}} }\left\{\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}}\:+\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}−\mathrm{1}\right\} \\ $$
Commented by zainal tanjung last updated on 23/Apr/20

$$\mathrm{thank}\:\mathrm{sir} \\ $$
