
Question Number 216742 by Tawa11 last updated on 17/Feb/25
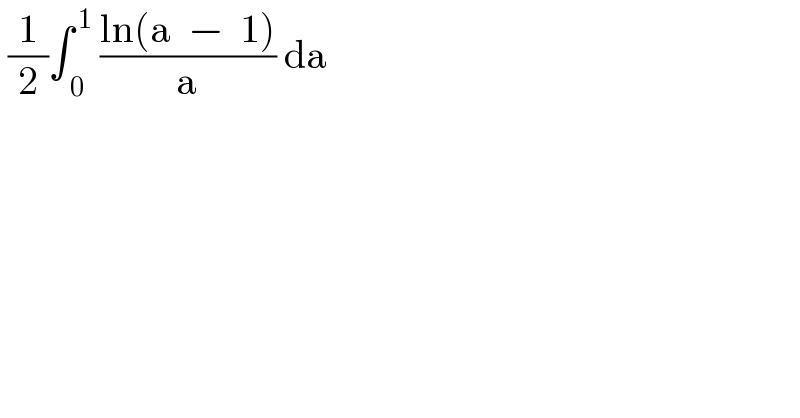
$$\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{a}\:\:−\:\:\mathrm{1}\right)}{\mathrm{a}}\:\mathrm{da} \\ $$
Answered by sniper237 last updated on 17/Feb/25
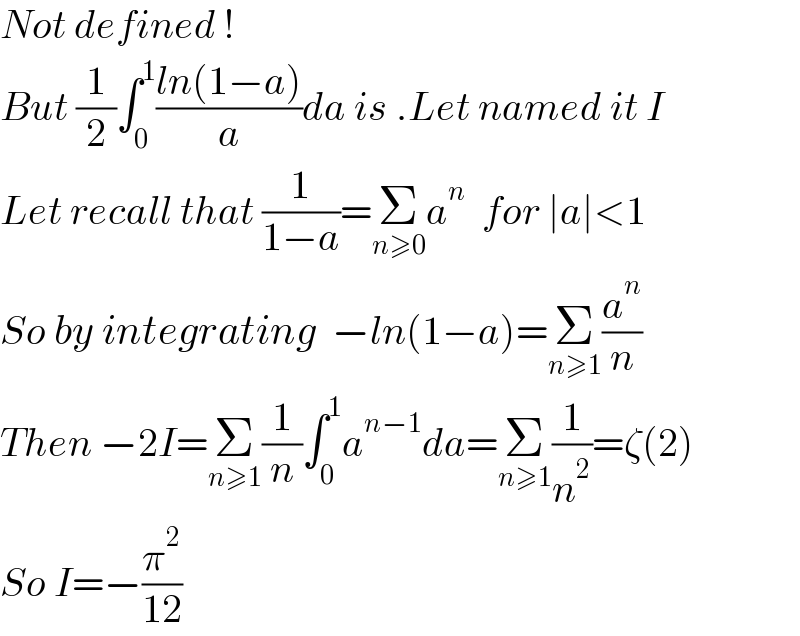
$${Not}\:{defined}\:! \\ $$$${But}\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{a}\right)}{{a}}{da}\:{is}\:.{Let}\:{named}\:{it}\:{I} \\ $$$${Let}\:{recall}\:{that}\:\frac{\mathrm{1}}{\mathrm{1}−{a}}=\underset{{n}\geqslant\mathrm{0}} {\sum}{a}^{{n}} \:\:{for}\:\mid{a}\mid<\mathrm{1} \\ $$$${So}\:{by}\:{integrating}\:\:−{ln}\left(\mathrm{1}−{a}\right)=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{{a}^{{n}} }{{n}}\: \\ $$$${Then}\:−\mathrm{2}{I}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} {a}^{{n}−\mathrm{1}} {da}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }=\zeta\left(\mathrm{2}\right) \\ $$$${So}\:{I}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
Commented by Tawa11 last updated on 17/Feb/25
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}. \\ $$
