
Question Number 68788 by mhmd last updated on 15/Sep/19

$$\int\mathrm{1}/\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} \:{dx} \\ $$
Commented by Prithwish sen last updated on 15/Sep/19
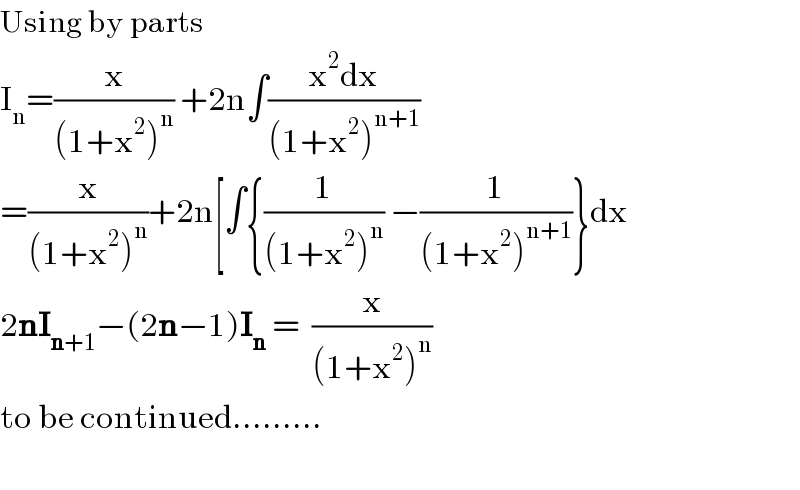
$$\mathrm{Using}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\mathrm{I}_{\mathrm{n}} =\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }\:+\mathrm{2n}\int\frac{\mathrm{x}^{\mathrm{2}} \mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}+\mathrm{1}} } \\ $$$$=\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }+\mathrm{2n}\left[\int\left\{\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }\:−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}+\mathrm{1}} }\right\}\mathrm{dx}\right. \\ $$$$\mathrm{2}\boldsymbol{\mathrm{nI}}_{\boldsymbol{\mathrm{n}}+\mathrm{1}} −\left(\mathrm{2}\boldsymbol{\mathrm{n}}−\mathrm{1}\right)\boldsymbol{\mathrm{I}}_{\boldsymbol{\mathrm{n}}} \:=\:\:\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{n}} }\: \\ $$$$\mathrm{to}\:\mathrm{be}\:\mathrm{continued}......... \\ $$$$ \\ $$
