Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 201229 by Calculusboy last updated on 02/Dec/23

∫ (1/( (√(1+Inx))))dx

$$\int\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\boldsymbol{{Inx}}}}\boldsymbol{{dx}} \\ $$

Commented by mnjuly1970 last updated on 02/Dec/23

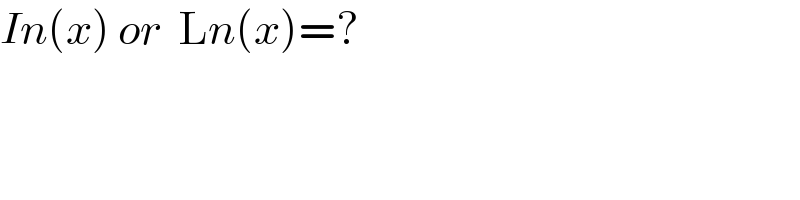
In(x) or Ln(x)=?

$${In}\left({x}\right)\:{or}\:\:\mathrm{L}{n}\left({x}\right)=? \\ $$

Commented by Calculusboy last updated on 02/Dec/23

the first one

$$\boldsymbol{{the}}\:\boldsymbol{{first}}\:\boldsymbol{{one}} \\ $$

Answered by witcher3 last updated on 02/Dec/23

ln(x)=t =∫(e^t /( (√(1+t)))) =∫(e^(((√((1+t))))^2 −1) /1).2d((√(1+t)));(√(1+t))=x_1 =2∫e^(x_1 ^2 −1) dx =(2/e)∫e^x_1 ^2 dx_1 ;x_1 =it=(2/( (√e)))i∫e^(−t^2 ) dt =(√(π/e)).i erfc(t) (2/( (√π)))∫_0 ^x e^(−t^2 ) dt=erfc(x) =i(√(π/e)).erfc(−ix_1 )+c ∫(dx/( (√(1+ln(x)))))=c+i(√((π/e).))erfc(−i(√(1+ln(x))));c∈R

$$\mathrm{ln}\left(\mathrm{x}\right)=\mathrm{t} \\ $$$$=\int\frac{\mathrm{e}^{\mathrm{t}} }{\:\sqrt{\mathrm{1}+\mathrm{t}}} \\ $$$$=\int\frac{\mathrm{e}^{\left(\sqrt{\left(\mathrm{1}+\mathrm{t}\right)}\right)^{\mathrm{2}} −\mathrm{1}} }{\mathrm{1}}.\mathrm{2d}\left(\sqrt{\mathrm{1}+\mathrm{t}}\right);\sqrt{\mathrm{1}+\mathrm{t}}=\mathrm{x}_{\mathrm{1}} \\ $$$$=\mathrm{2}\int\mathrm{e}^{\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{1}} \mathrm{dx} \\ $$$$=\frac{\mathrm{2}}{\mathrm{e}}\int\mathrm{e}^{\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} } \mathrm{dx}_{\mathrm{1}} ;\mathrm{x}_{\mathrm{1}} =\mathrm{it}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{e}}}\mathrm{i}\int\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt} \\ $$$$=\sqrt{\frac{\pi}{\mathrm{e}}}.\mathrm{i}\:\mathrm{erfc}\left(\mathrm{t}\right) \\ $$$$\frac{\mathrm{2}}{\:\sqrt{\pi}}\int_{\mathrm{0}} ^{\mathrm{x}} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}=\mathrm{erfc}\left(\mathrm{x}\right) \\ $$$$=\mathrm{i}\sqrt{\frac{\pi}{\mathrm{e}}}.\mathrm{erfc}\left(−\mathrm{ix}_{\mathrm{1}} \right)+\mathrm{c} \\ $$$$\int\frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{ln}\left(\mathrm{x}\right)}}=\mathrm{c}+\mathrm{i}\sqrt{\frac{\pi}{\mathrm{e}}.}\mathrm{erfc}\left(−\mathrm{i}\sqrt{\mathrm{1}+\mathrm{ln}\left(\mathrm{x}\right)}\right);\mathrm{c}\in\mathbb{R} \\ $$$$ \\ $$

Commented by Calculusboy last updated on 02/Dec/23

thanks sir

$$\boldsymbol{{thanks}}\:\boldsymbol{{sir}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com