
Question Number 46245 by rpseelam last updated on 23/Oct/18
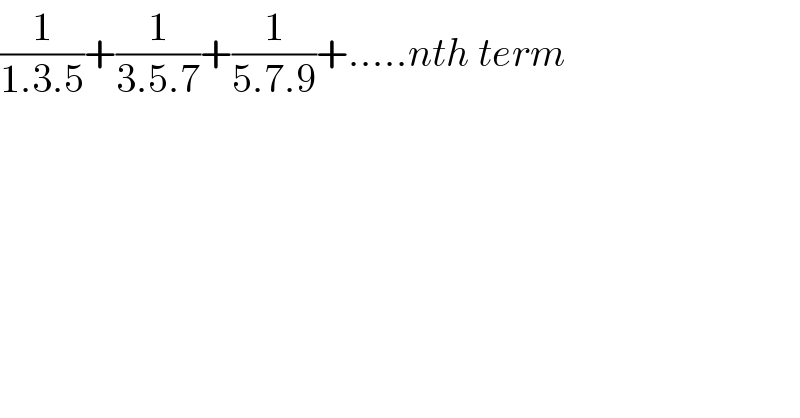
$$\frac{\mathrm{1}}{\mathrm{1}.\mathrm{3}.\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{3}.\mathrm{5}.\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{5}.\mathrm{7}.\mathrm{9}}+.....{nth}\:{term} \\ $$
Commented by maxmathsup by imad last updated on 23/Oct/18

$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{3}\right)\left(\mathrm{2}{k}+\mathrm{5}\right)}\:\:\:{let}\:{find}\:\:{S}_{{n}} \:\:\:{let}\:{decompose} \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{2}{x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{3}\right)\left(\mathrm{2}{x}+\mathrm{5}\right)}\:\Rightarrow{F}\left({x}\right)=\frac{{a}}{\mathrm{2}{x}+\mathrm{1}}\:+\frac{{b}}{\mathrm{2}{x}+\mathrm{3}}\:+\frac{{c}}{\mathrm{2}{x}+\mathrm{5}} \\ $$$${a}\:={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\left(\mathrm{2}{x}+\mathrm{1}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{2}.\mathrm{4}}\:=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${b}={lim}_{{x}\rightarrow−\frac{\mathrm{3}}{\mathrm{2}}} \:\:\:\left(\mathrm{2}{x}+\mathrm{3}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{\left(−\mathrm{2}\right).\mathrm{2}}\:=−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${c}={lim}_{{x}\rightarrow−\frac{\mathrm{5}}{\mathrm{2}}} \:\:\left(\mathrm{2}{x}+\mathrm{5}\right){F}\left({x}\right)=\:\frac{\mathrm{1}}{\left(−\mathrm{4}\right).\left(−\mathrm{2}\right)}\:=\frac{\mathrm{1}}{\mathrm{8}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{x}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{x}+\mathrm{3}\right)}\:+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{x}+\mathrm{5}\right)}\:\Rightarrow \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{8}}\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{8}}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{5}}\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{3}}\:=_{{k}={j}−\mathrm{1}} \:\:\:\sum_{{j}=\mathrm{1}} ^{{n}+\mathrm{1}} \:\:\frac{\mathrm{1}}{\mathrm{2}{j}+\mathrm{1}}\:=\sum_{{j}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{j}+\mathrm{1}}\:−\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{5}}\:=_{{k}={j}−\mathrm{2}} \:\sum_{{j}=\mathrm{2}} ^{{n}+\mathrm{2}} \:\:\frac{\mathrm{1}}{\mathrm{2}{j}\:+\mathrm{1}}\:=\sum_{{j}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{j}+\mathrm{1}}\:−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{5}} \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{8}}\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:\sum_{{j}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{j}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$+\frac{\mathrm{1}}{\mathrm{8}}\sum_{{j}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{j}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left(−\frac{\mathrm{4}}{\mathrm{3}}\right)\:+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{n}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{n}+\mathrm{5}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:−\frac{\mathrm{1}}{\mathrm{6}}\:\:−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{n}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{n}+\right)}\:+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{n}+\mathrm{5}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\:−\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{n}+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{8}\left(\mathrm{2}{n}+\mathrm{5}\right)}\:=\frac{\mathrm{1}}{\mathrm{12}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{5}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left\{\frac{−\mathrm{4}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{5}\right)}\right\}\:=\frac{\mathrm{1}}{\mathrm{12}}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{5}\right)}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 23/Oct/18
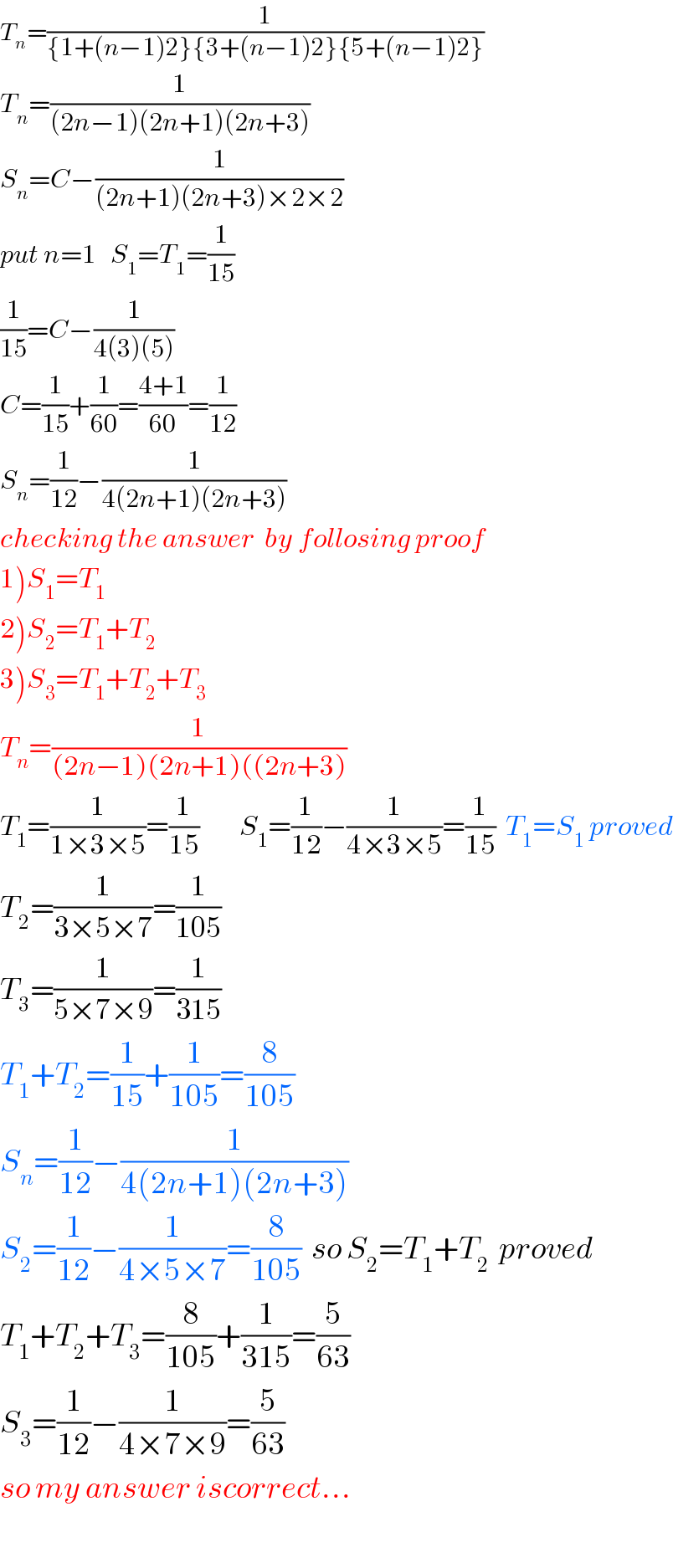
$${T}_{{n}} =\frac{\mathrm{1}}{\left\{\mathrm{1}+\left({n}−\mathrm{1}\right)\mathrm{2}\right\}\left\{\mathrm{3}+\left({n}−\mathrm{1}\right)\mathrm{2}\right\}\left\{\mathrm{5}+\left({n}−\mathrm{1}\right)\mathrm{2}\right\}} \\ $$$${T}_{{n}} =\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$${S}_{{n}} ={C}−\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)×\mathrm{2}×\mathrm{2}} \\ $$$${put}\:{n}=\mathrm{1}\:\:\:{S}_{\mathrm{1}} ={T}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{15}} \\ $$$$\frac{\mathrm{1}}{\mathrm{15}}={C}−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{3}\right)\left(\mathrm{5}\right)} \\ $$$${C}=\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{60}}=\frac{\mathrm{4}+\mathrm{1}}{\mathrm{60}}=\frac{\mathrm{1}}{\mathrm{12}} \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$${checking}\:{the}\:{answer}\:\:{by}\:{follosing}\:{proof} \\ $$$$\left.\mathrm{1}\right){S}_{\mathrm{1}} ={T}_{\mathrm{1}} \\ $$$$\left.\mathrm{2}\right){S}_{\mathrm{2}} ={T}_{\mathrm{1}} +{T}_{\mathrm{2}} \\ $$$$\left.\mathrm{3}\right){S}_{\mathrm{3}} ={T}_{\mathrm{1}} +{T}_{\mathrm{2}} +{T}_{\mathrm{3}} \\ $$$${T}_{{n}} =\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\left(\mathrm{2}{n}+\mathrm{3}\right)\right.} \\ $$$${T}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}×\mathrm{3}×\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{15}}\:\:\:\:\:\:\:\:{S}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{4}×\mathrm{3}×\mathrm{5}}=\frac{\mathrm{1}}{\mathrm{15}}\:\:{T}_{\mathrm{1}} ={S}_{\mathrm{1}} \:{proved} \\ $$$${T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{3}×\mathrm{5}×\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{105}} \\ $$$${T}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{5}×\mathrm{7}×\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{315}} \\ $$$${T}_{\mathrm{1}} +{T}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{15}}+\frac{\mathrm{1}}{\mathrm{105}}=\frac{\mathrm{8}}{\mathrm{105}} \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{2}{n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{3}\right)} \\ $$$${S}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{4}×\mathrm{5}×\mathrm{7}}=\frac{\mathrm{8}}{\mathrm{105}}\:\:{so}\:{S}_{\mathrm{2}} ={T}_{\mathrm{1}} +{T}_{\mathrm{2}} \:\:{proved} \\ $$$${T}_{\mathrm{1}} +{T}_{\mathrm{2}} +{T}_{\mathrm{3}} =\frac{\mathrm{8}}{\mathrm{105}}+\frac{\mathrm{1}}{\mathrm{315}}=\frac{\mathrm{5}}{\mathrm{63}} \\ $$$${S}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{12}}−\frac{\mathrm{1}}{\mathrm{4}×\mathrm{7}×\mathrm{9}}=\frac{\mathrm{5}}{\mathrm{63}} \\ $$$${so}\:{my}\:{answer}\:{iscorrect}... \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Oct/18

$${my}\:{ans}\:{is}\:{correct}... \\ $$
Commented by rpseelam last updated on 24/Oct/18
$${that}\:{is}\:{excellent}\:{sir}.\:{thanks} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 24/Oct/18

$${most}\:{welcome}... \\ $$
