Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 189559 by 073 last updated on 18/Mar/23

(−1)^(1/3) =? ((−1))^(1/3) =?

$$\:\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =? \\ $$$$\sqrt[{\mathrm{3}}]{−\mathrm{1}}=? \\ $$

Answered by Frix last updated on 18/Mar/23

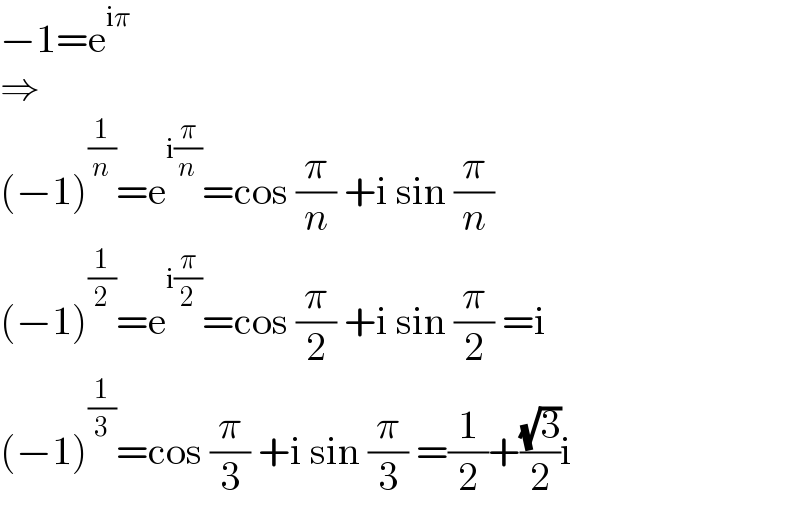
−1=e^(iπ) ⇒ (−1)^(1/n) =e^(i(π/n)) =cos (π/n) +i sin (π/n) (−1)^(1/2) =e^(i(π/2)) =cos (π/2) +i sin (π/2) =i (−1)^(1/3) =cos (π/3) +i sin (π/3) =(1/2)+((√3)/2)i

$$−\mathrm{1}=\mathrm{e}^{\mathrm{i}\pi} \\ $$$$\Rightarrow \\ $$$$\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{{n}}} =\mathrm{e}^{\mathrm{i}\frac{\pi}{{n}}} =\mathrm{cos}\:\frac{\pi}{{n}}\:+\mathrm{i}\:\mathrm{sin}\:\frac{\pi}{{n}} \\ $$$$\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} =\mathrm{e}^{\mathrm{i}\frac{\pi}{\mathrm{2}}} =\mathrm{cos}\:\frac{\pi}{\mathrm{2}}\:+\mathrm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{2}}\:=\mathrm{i} \\ $$$$\left(−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{cos}\:\frac{\pi}{\mathrm{3}}\:+\mathrm{i}\:\mathrm{sin}\:\frac{\pi}{\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\mathrm{i} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com