Question and Answers Forum

All Questions      Topic List

Probability and Statistics Questions

Previous in All Question      Next in All Question      

Previous in Probability and Statistics      Next in Probability and Statistics      

Question Number 207665 by efronzo1 last updated on 22/May/24

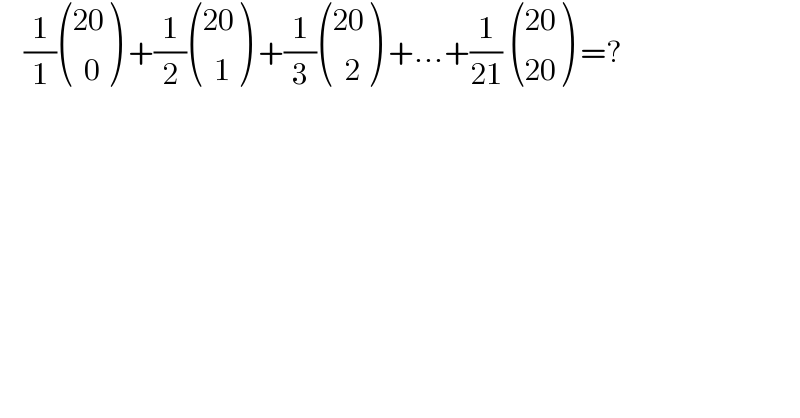
(1/1) (((20)),(( 0)) ) +(1/2) (((20)),(( 1)) ) +(1/3) (((20)),(( 2)) ) +...+(1/(21)) (((20)),((20)) ) =?

$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{1}}\begin{pmatrix}{\mathrm{20}}\\{\:\:\mathrm{0}}\end{pmatrix}\:+\frac{\mathrm{1}}{\mathrm{2}}\begin{pmatrix}{\mathrm{20}}\\{\:\:\mathrm{1}}\end{pmatrix}\:+\frac{\mathrm{1}}{\mathrm{3}}\begin{pmatrix}{\mathrm{20}}\\{\:\:\mathrm{2}}\end{pmatrix}\:+...+\frac{\mathrm{1}}{\mathrm{21}}\:\begin{pmatrix}{\mathrm{20}}\\{\mathrm{20}}\end{pmatrix}\:=? \\ $$

Answered by Tinku Tara last updated on 22/May/24

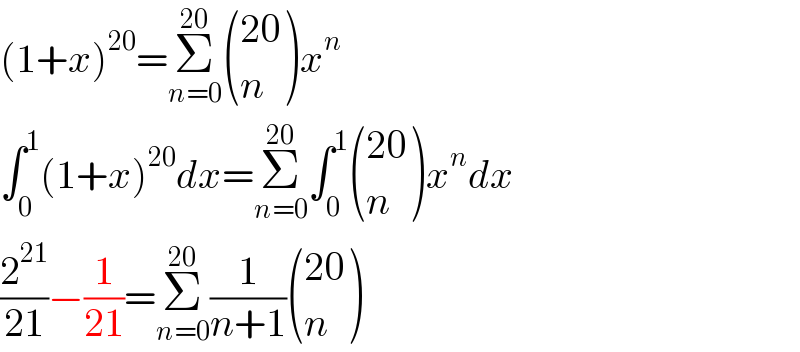
(1+x)^(20) =Σ_(n=0) ^(20) (((20)),(n) )x^n ∫_0 ^1 (1+x)^(20) dx=Σ_(n=0) ^(20) ∫_0 ^1 (((20)),(n) )x^n dx (2^(21) /(21))−(1/(21))=Σ_(n=0) ^(20) (1/(n+1)) (((20)),(n) )

$$\left(\mathrm{1}+{x}\right)^{\mathrm{20}} =\underset{{n}=\mathrm{0}} {\overset{\mathrm{20}} {\sum}}\begin{pmatrix}{\mathrm{20}}\\{{n}}\end{pmatrix}{x}^{{n}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}\right)^{\mathrm{20}} {dx}=\underset{{n}=\mathrm{0}} {\overset{\mathrm{20}} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} \begin{pmatrix}{\mathrm{20}}\\{{n}}\end{pmatrix}{x}^{{n}} {dx} \\ $$$$\frac{\mathrm{2}^{\mathrm{21}} }{\mathrm{21}}−\frac{\mathrm{1}}{\mathrm{21}}=\underset{{n}=\mathrm{0}} {\overset{\mathrm{20}} {\sum}}\frac{\mathrm{1}}{{n}+\mathrm{1}}\begin{pmatrix}{\mathrm{20}}\\{{n}}\end{pmatrix} \\ $$

Commented by MM42 last updated on 22/May/24

∫_0 ^1 (1+x)^(20) dx=(((1+x)^(21) )/(21)) ]_0 ^1 =((2^(21) −1)/(21))

$$\left.\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{x}\right)^{\mathrm{20}} {dx}=\frac{\left(\mathrm{1}+{x}\right)^{\mathrm{21}} }{\mathrm{21}}\:\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}^{\mathrm{21}} −\mathrm{1}}{\mathrm{21}} \\ $$$$ \\ $$

Commented by Tinku Tara last updated on 22/May/24

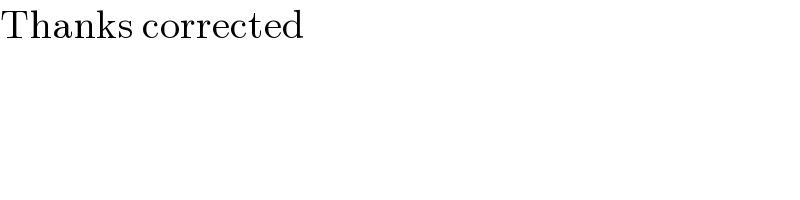
Thanks corrected

$$\mathrm{Thanks}\:\mathrm{corrected} \\ $$

Commented by MM42 last updated on 23/May/24

⋛

$$\:\cancel{\lesseqgtr} \\ $$

Answered by Frix last updated on 22/May/24

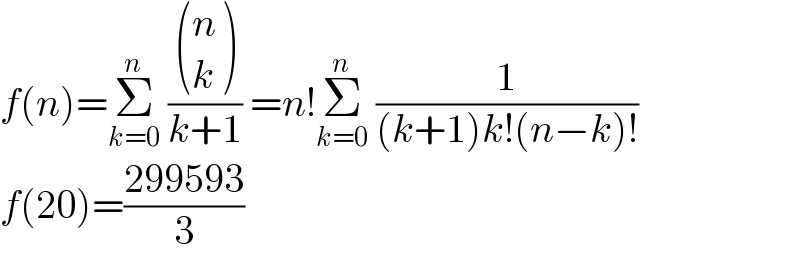
f(n)=Σ_(k=0) ^n ( ((n),(k) )/(k+1)) =n!Σ_(k=0) ^n (1/((k+1)k!(n−k)!)) f(20)=((299593)/3)

$${f}\left({n}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:\frac{\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}}{{k}+\mathrm{1}}\:={n}!\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right){k}!\left({n}−{k}\right)!} \\ $$$${f}\left(\mathrm{20}\right)=\frac{\mathrm{299593}}{\mathrm{3}} \\ $$

Answered by mr W last updated on 22/May/24

n=20 Σ_(k=0) ^n (1/(k+1)) ((n),(k) ) =Σ_(k=0) ^n ((n!)/((k+1)k!(n−k)!)) =(1/((n+1)))Σ_(k=0) ^n (((n+1)!)/((k+1)!(n−k)!)) =(1/((n+1)))Σ_(k=0) ^n (((n+1)!)/((k+1)!(n+1−k−1)!)) =(1/((n+1)))Σ_(r=1) ^(n+1) (((n+1)!)/(r!(n+1−r)!)) =(1/((n+1)))[Σ_(r=0) ^(n+1) (((n+1)!)/(r!(n+1−r)!))−1] =(1/((n+1)))[Σ_(r=0) ^(n+1) (((n+1)),(r) )−1] =(1/((n+1)))(2^(n+1) −1) =((2^(n+1) −1)/(n+1))=((2^(21) −1)/(21)) ✓

$${n}=\mathrm{20} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}+\mathrm{1}}\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{n}!}{\left({k}+\mathrm{1}\right){k}!\left({n}−{k}\right)!} \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left({n}+\mathrm{1}\right)!}{\left({k}+\mathrm{1}\right)!\left({n}−{k}\right)!} \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{\left({n}+\mathrm{1}\right)!}{\left({k}+\mathrm{1}\right)!\left({n}+\mathrm{1}−{k}−\mathrm{1}\right)!} \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\underset{{r}=\mathrm{1}} {\overset{{n}+\mathrm{1}} {\sum}}\frac{\left({n}+\mathrm{1}\right)!}{{r}!\left({n}+\mathrm{1}−{r}\right)!} \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\left[\underset{{r}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\frac{\left({n}+\mathrm{1}\right)!}{{r}!\left({n}+\mathrm{1}−{r}\right)!}−\mathrm{1}\right] \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\left[\underset{{r}=\mathrm{0}} {\overset{{n}+\mathrm{1}} {\sum}}\begin{pmatrix}{{n}+\mathrm{1}}\\{{r}}\end{pmatrix}−\mathrm{1}\right] \\ $$$$=\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)}\left(\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}^{{n}+\mathrm{1}} −\mathrm{1}}{{n}+\mathrm{1}}=\frac{\mathrm{2}^{\mathrm{21}} −\mathrm{1}}{\mathrm{21}}\:\checkmark \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com