
Question Number 174341 by behi834171 last updated on 31/Jul/22
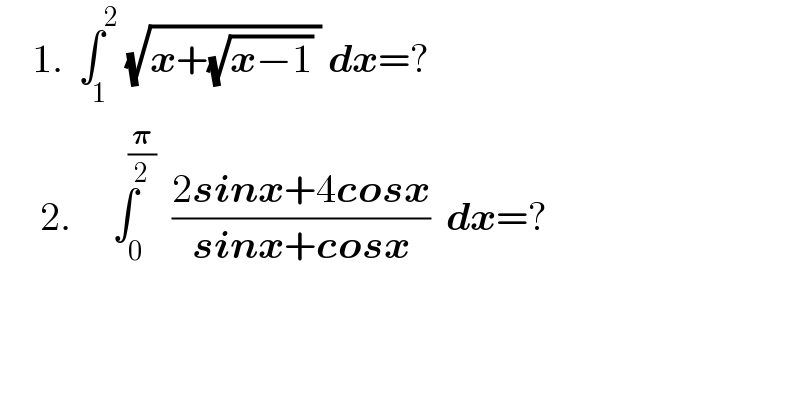
$$\:\:\:\:\mathrm{1}.\underset{\:\:\:\:\mathrm{1}} {\overset{\:\:\:\:\:\:\:\:\:\:\mathrm{2}} {\int}}\:\sqrt{\boldsymbol{{x}}+\sqrt{\boldsymbol{{x}}−\mathrm{1}}\:}\:\boldsymbol{{dx}}=? \\ $$$$\:\:\:\:\:\mathrm{2}.\:\:\:\underset{\:\:\:\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\int}}\:\:\frac{\mathrm{2}\boldsymbol{{sinx}}+\mathrm{4}\boldsymbol{{cosx}}}{\boldsymbol{{sinx}}+\boldsymbol{{cosx}}}\:\:\boldsymbol{{dx}}=? \\ $$
Commented by mnjuly1970 last updated on 30/Jul/22

$$\:\mathrm{2}.\left(\:\:\:\mathrm{3}\pi/\mathrm{2}\:\right) \\ $$
Answered by MJS_new last updated on 30/Jul/22
![1. ∫(√(x+(√(x−1))))dx= [t=(√(x−1))+(1/2) → dx=(2t−1)dt] =(1/2)∫(2t−1)(√(4t^2 +3))dt= [u=((2t+(√(4t^2 +3)))/( (√3))) → dt=((√(4t^2 +3))/(2u))du] =∫(((3(√3))/(32))u^2 −(3/(16))u+((3(√3))/(32))−(3/8)u^(−1) −((3(√3))/(32))u^(−2) −(3/(16))u^(−3) −((3(√3))/(32))u^(−4) )du the rest is easy](Q174344.png)
$$\mathrm{1}. \\ $$$$\int\sqrt{{x}+\sqrt{{x}−\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\:\rightarrow\:{dx}=\left(\mathrm{2}{t}−\mathrm{1}\right){dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{2}{t}−\mathrm{1}\right)\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}{dt}= \\ $$$$\:\:\:\:\:\left[{u}=\frac{\mathrm{2}{t}+\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}}{\:\sqrt{\mathrm{3}}}\:\rightarrow\:{dt}=\frac{\sqrt{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}}}{\mathrm{2}{u}}{du}\right] \\ $$$$=\int\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}{u}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{16}}{u}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}−\frac{\mathrm{3}}{\mathrm{8}}{u}^{−\mathrm{1}} −\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}{u}^{−\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{16}}{u}^{−\mathrm{3}} −\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}{u}^{−\mathrm{4}} \right){du} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
Commented by behi834171 last updated on 30/Jul/22
$${very}\:{nice}! \\ $$$$\:{thank}\:{you}\:{so}\:{much}\:{dear}\:{master}. \\ $$
Answered by Frix last updated on 30/Jul/22
![∫_0 ^(π/2) ((2sin x +4cos x)/(sin x +cos x))dx= =3∫_0 ^(π/2) dx−∫_0 ^(π/2) ((sin x −cos x)/(sin x +cos x))dx 3∫_0 ^(π/2) dx=((3π)/2) −∫_0 ^(π/2) ((sin x −cos x)/(sin x +cos x))dx= =∫_0 ^(π/2) ((d[sin x +cos x])/(sin x +cos x))= =[ln ∣sin x +cos x∣]_0 ^(π/2) =0 ⇒ answer is ((3π)/2)](Q174352.png)
$$\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{\mathrm{2sin}\:{x}\:+\mathrm{4cos}\:{x}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{dx}= \\ $$$$=\mathrm{3}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}{dx}−\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{dx} \\ $$$$\mathrm{3}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}{dx}=\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$$−\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{dx}= \\ $$$$=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{{d}\left[\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\right]}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}= \\ $$$$=\left[\mathrm{ln}\:\mid\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\mid\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$
Commented by behi834171 last updated on 30/Jul/22
$${thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$$${your}\:{answer}\:{is}\:{true}. \\ $$
Answered by behi834171 last updated on 31/Jul/22
![let: x−1=t^2 ⇒dx=2tdt I=∫2t(√(t^2 +1+t))dt=∫(2t+1−1)(√(t^2 +t+1))dt= =∫(2t+1)(√(t^2 +t+1))dt−∫(√(t^2 +t+1))dt=I_1 +I_2 I_1 =(2/3)(t^2 +t+1)^(3/2) +const. I_2 =∫(√((t+(1/2))^2 +(((√3)/2))^2 ))dt= =((2t+1)/4)(√(t^2 +t+1))+(3/8)sinh^(−1) (((2t+1)/( (√3))))+const. ⇒I=(2/3)(x+(√(x−1)))^(3/2) +(((2(√(x−1))+1)/4)).(√(x+(√(x−1))))+ + (3/8)sinh^(−1) (((2(√(x−1))+1)/( (√3))))+const. ■ [I_1 =2(√3)−(2/3)=((6(√3)−2)/3) I_2 =((3(√(3 ))−1)/4)+(3/(10))=((15(√3)+1)/(20)) ⇒I=I_1 +I_2 =((165(√3)−37)/(60))]](Q174399.png)
$${let}:\:{x}−\mathrm{1}={t}^{\mathrm{2}} \Rightarrow\boldsymbol{{dx}}=\mathrm{2}\boldsymbol{{tdt}} \\ $$$$\boldsymbol{{I}}=\int\mathrm{2}\boldsymbol{{t}}\sqrt{\boldsymbol{{t}}^{\mathrm{2}} +\mathrm{1}+\boldsymbol{{t}}}\boldsymbol{{dt}}=\int\left(\mathrm{2}\boldsymbol{{t}}+\mathrm{1}−\mathrm{1}\right)\sqrt{\boldsymbol{{t}}^{\mathrm{2}} +\boldsymbol{{t}}+\mathrm{1}}\boldsymbol{{dt}}= \\ $$$$=\int\left(\mathrm{2}\boldsymbol{{t}}+\mathrm{1}\right)\sqrt{\boldsymbol{{t}}^{\mathrm{2}} +\boldsymbol{{t}}+\mathrm{1}}\boldsymbol{{dt}}−\int\sqrt{\boldsymbol{{t}}^{\mathrm{2}} +\boldsymbol{{t}}+\mathrm{1}}\boldsymbol{{dt}}=\boldsymbol{{I}}_{\mathrm{1}} +\boldsymbol{{I}}_{\mathrm{2}} \\ $$$$\boldsymbol{{I}}_{\mathrm{1}} =\frac{\mathrm{2}}{\mathrm{3}}\left(\boldsymbol{{t}}^{\mathrm{2}} +\boldsymbol{{t}}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\boldsymbol{{const}}. \\ $$$$\boldsymbol{{I}}_{\mathrm{2}} =\int\sqrt{\left(\boldsymbol{{t}}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} }\boldsymbol{{dt}}= \\ $$$$=\frac{\mathrm{2}\boldsymbol{{t}}+\mathrm{1}}{\mathrm{4}}\sqrt{\boldsymbol{{t}}^{\mathrm{2}} +\boldsymbol{{t}}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{8}}\boldsymbol{{sinh}}^{−\mathrm{1}} \left(\frac{\mathrm{2}\boldsymbol{{t}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\boldsymbol{{const}}. \\ $$$$\Rightarrow\boldsymbol{{I}}=\frac{\mathrm{2}}{\mathrm{3}}\left(\boldsymbol{{x}}+\sqrt{\boldsymbol{{x}}−\mathrm{1}}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\left(\frac{\mathrm{2}\sqrt{\boldsymbol{{x}}−\mathrm{1}}+\mathrm{1}}{\mathrm{4}}\right).\sqrt{\boldsymbol{{x}}+\sqrt{\boldsymbol{{x}}−\mathrm{1}}}+ \\ $$$$+ \\ $$$$\frac{\mathrm{3}}{\mathrm{8}}\boldsymbol{{sinh}}^{−\mathrm{1}} \:\left(\frac{\mathrm{2}\sqrt{\boldsymbol{{x}}−\mathrm{1}}+\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\boldsymbol{{const}}.\:\:\blacksquare \\ $$$$\left[{I}_{\mathrm{1}} =\mathrm{2}\sqrt{\mathrm{3}}−\frac{\mathrm{2}}{\mathrm{3}}=\frac{\mathrm{6}\sqrt{\mathrm{3}}−\mathrm{2}}{\mathrm{3}}\right. \\ $$$${I}_{\mathrm{2}} =\frac{\mathrm{3}\sqrt{\mathrm{3}\:}−\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{10}}=\frac{\mathrm{15}\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{20}} \\ $$$$\left.\Rightarrow\boldsymbol{\mathrm{I}}=\boldsymbol{{I}}_{\mathrm{1}} +\boldsymbol{{I}}_{\mathrm{2}} =\frac{\mathrm{165}\sqrt{\mathrm{3}}−\mathrm{37}}{\mathrm{60}}\right] \\ $$
Commented by peter frank last updated on 01/Aug/22

$$\mathrm{thanks} \\ $$
