
Question Number 136757 by Dwaipayan Shikari last updated on 25/Mar/21
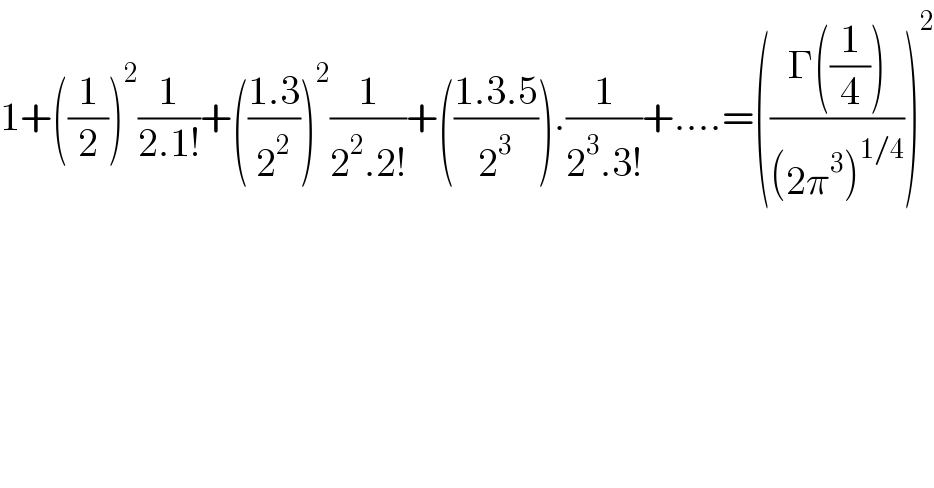
$$\mathrm{1}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}.\mathrm{1}!}+\left(\frac{\mathrm{1}.\mathrm{3}}{\mathrm{2}^{\mathrm{2}} }\right)^{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} .\mathrm{2}!}+\left(\frac{\mathrm{1}.\mathrm{3}.\mathrm{5}}{\mathrm{2}^{\mathrm{3}} }\right).\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} .\mathrm{3}!}+....=\left(\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\left(\mathrm{2}\pi^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{4}} }\right)^{\mathrm{2}} \\ $$
Answered by mindispower last updated on 25/Mar/21

$$\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}^{\mathrm{3}{n}} .{n}!\:}\:\:...? \\ $$$$ \\ $$
