
Question Number 89064 by john santu last updated on 15/Apr/20
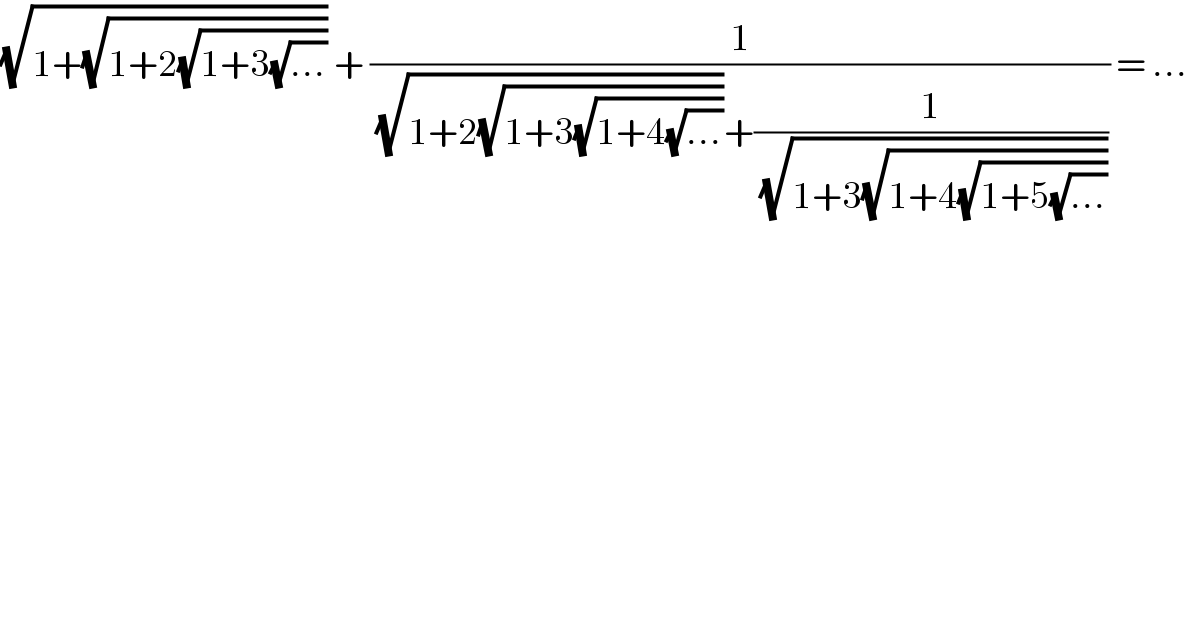
$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{...}}}}\:+\:\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{...}}}}+\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+\mathrm{5}\sqrt{...}}}}}}\:=\:... \\ $$
Answered by M±th+et£s last updated on 16/Apr/20
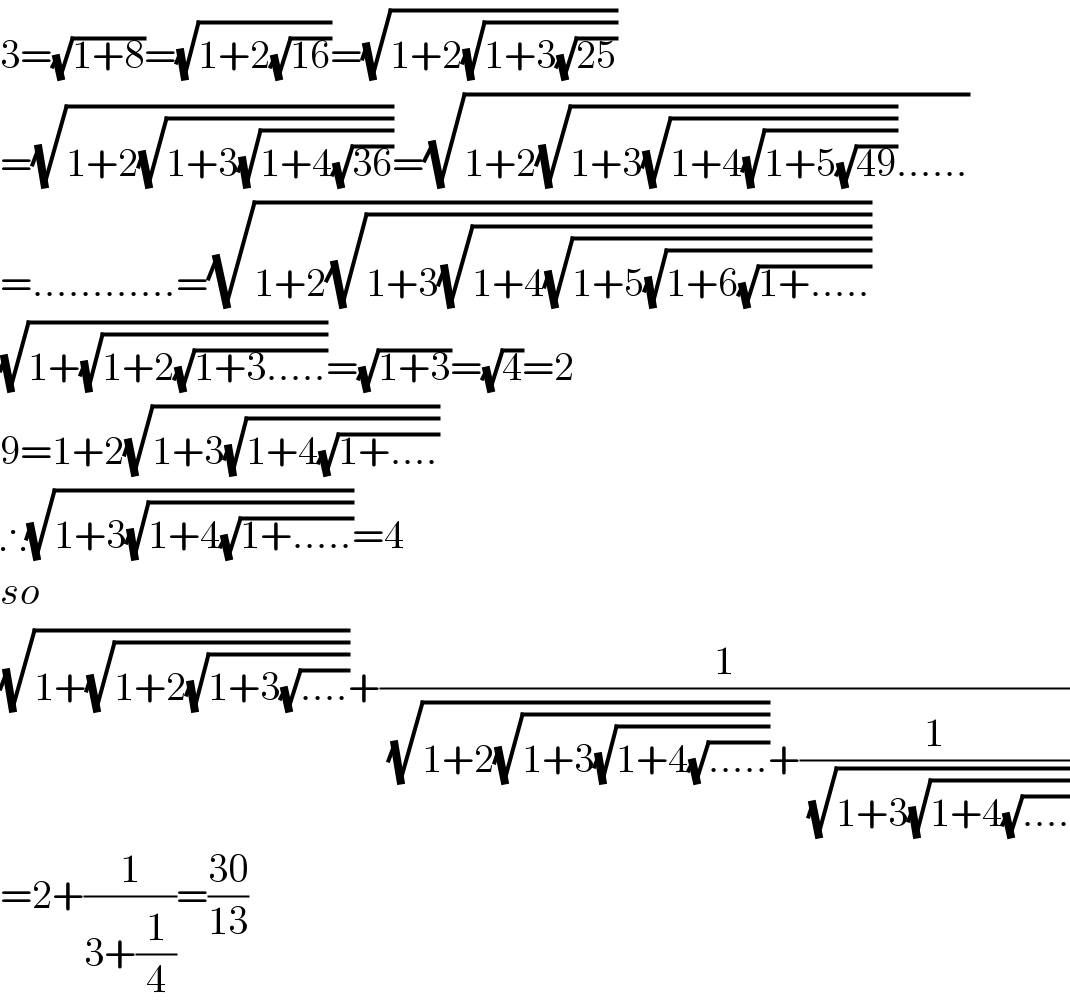
$$\mathrm{3}=\sqrt{\mathrm{1}+\mathrm{8}}=\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{16}}}=\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{25}}}} \\ $$$$=\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{36}}}}}=\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+\mathrm{5}\sqrt{\mathrm{49}}}}}......} \\ $$$$=............=\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+\mathrm{5}\sqrt{\mathrm{1}+\mathrm{6}\sqrt{\mathrm{1}+.....}}}}}} \\ $$$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}.....}}}=\sqrt{\mathrm{1}+\mathrm{3}}=\sqrt{\mathrm{4}}=\mathrm{2} \\ $$$$\mathrm{9}=\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+....}}} \\ $$$$\therefore\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{\mathrm{1}+.....}}}=\mathrm{4} \\ $$$${so} \\ $$$$\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{....}}}}+\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{.....}}}}+\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{3}\sqrt{\mathrm{1}+\mathrm{4}\sqrt{....}}}}} \\ $$$$=\mathrm{2}+\frac{\mathrm{1}}{\mathrm{3}+\frac{\mathrm{1}}{\mathrm{4}}}=\frac{\mathrm{30}}{\mathrm{13}} \\ $$
