Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 83931 by john santu last updated on 08/Mar/20

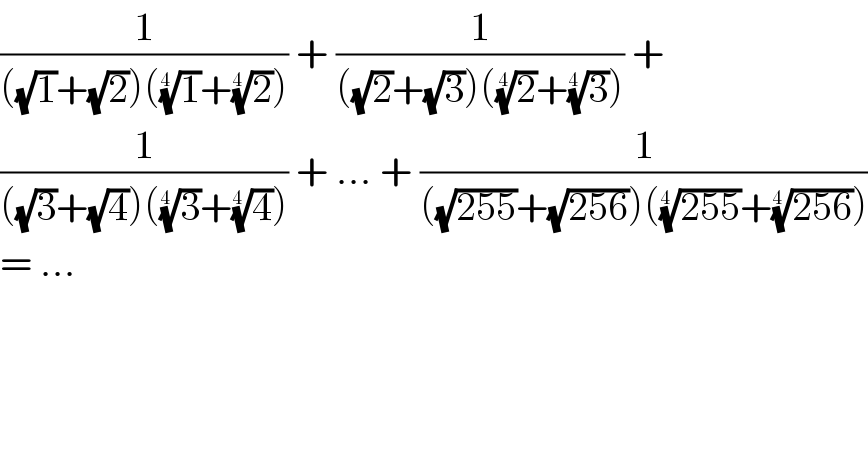
(1/(((√1)+(√2))((1)^(1/(4 )) +(2)^(1/(4 )) ))) + (1/(((√2)+(√3))((2)^(1/( 4)) +(3)^(1/(4 )) ))) + (1/(((√3)+(√4))((3)^(1/(4 )) +(4)^(1/(4 )) ))) + ... + (1/(((√(255))+(√(256)))(((255))^(1/(4 )) +((256))^(1/(4 )) ))) = ...

$$\frac{\mathrm{1}}{\left(\sqrt{\mathrm{1}}+\sqrt{\mathrm{2}}\right)\left(\sqrt[{\mathrm{4}\:}]{\mathrm{1}}+\sqrt[{\mathrm{4}\:}]{\mathrm{2}}\right)}\:+\:\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}\right)\left(\sqrt[{\:\mathrm{4}}]{\mathrm{2}}+\sqrt[{\mathrm{4}\:}]{\mathrm{3}}\right)}\:+ \\ $$$$\frac{\mathrm{1}}{\left(\sqrt{\mathrm{3}}+\sqrt{\mathrm{4}}\right)\left(\sqrt[{\mathrm{4}\:}]{\mathrm{3}}+\sqrt[{\mathrm{4}\:}]{\mathrm{4}}\right)}\:+\:...\:+\:\frac{\mathrm{1}}{\left(\sqrt{\mathrm{255}}+\sqrt{\mathrm{256}}\right)\left(\sqrt[{\mathrm{4}\:}]{\mathrm{255}}+\sqrt[{\mathrm{4}\:}]{\mathrm{256}}\right)} \\ $$$$=\:...\: \\ $$

Commented by john santu last updated on 08/Mar/20

yes. the answer 3

$$\mathrm{yes}.\:\mathrm{the}\:\mathrm{answer}\:\mathrm{3} \\ $$

Answered by TANMAY PANACEA last updated on 08/Mar/20

T_r =(1/(((√r) +(√(r+1)) )((r)^(1/4) +((r+1)))^(1/4) )) S=Σ_(r=1) ^(255) T_r T_r =(((r+1)−r)/D_r )=(((√(r+1)) −(√r))/((((r+1))^(1/4) +(r)^(1/4) )))=(((((r+1))^(1/4) +(r)^(1/4) )×(((r+1))^(1/4) −(r)^(1/4) ))/((((r+1))^(1/4) +(r)^(1/4) ))) T_r =((r+1))^(1/4) −(r)^(1/4) so Σ_(r=1) ^(255) T_r =0 pls check←it is my error so pls ignore... editing... T_r =((r+1))^(1/4) −(r)^(1/4) T_1 =(2)^(1/4) −(1)^(1/4) T_2 =(3)^(1/4) −(2)^(1/4) ... ... T_(255) =((256))^(1/4) −((255))^(1/4) S=((256))^(1/4) −(1)^(1/4) =4−1=3

$${T}_{{r}} =\frac{\mathrm{1}}{\left(\sqrt{{r}}\:+\sqrt{{r}+\mathrm{1}}\:\right)\left(\sqrt[{\mathrm{4}}]{{r}}\:+\sqrt[{\mathrm{4}}]{\left.{r}+\mathrm{1}\right)}\right.} \\ $$$${S}=\underset{{r}=\mathrm{1}} {\overset{\mathrm{255}} {\sum}}{T}_{{r}} \\ $$$${T}_{{r}} =\frac{\left({r}+\mathrm{1}\right)−{r}}{{D}_{{r}} }=\frac{\sqrt{{r}+\mathrm{1}}\:−\sqrt{{r}}}{\left(\sqrt[{\mathrm{4}}]{{r}+\mathrm{1}}\:+\sqrt[{\mathrm{4}}]{{r}}\:\right)}=\frac{\left(\sqrt[{\mathrm{4}}]{{r}+\mathrm{1}}\:+\sqrt[{\mathrm{4}}]{{r}}\:\right)×\left(\sqrt[{\mathrm{4}}]{{r}+\mathrm{1}}\:−\sqrt[{\mathrm{4}}]{{r}}\:\right)}{\left(\sqrt[{\mathrm{4}}]{{r}+\mathrm{1}}\:+\sqrt[{\mathrm{4}}]{{r}}\:\right)} \\ $$$${T}_{{r}} =\sqrt[{\mathrm{4}}]{{r}+\mathrm{1}}\:−\sqrt[{\mathrm{4}}]{{r}}\: \\ $$$${so}\:\underset{{r}=\mathrm{1}} {\overset{\mathrm{255}} {\sum}}{T}_{{r}} \:=\mathrm{0}\:\:\:\:\boldsymbol{{pls}}\:\boldsymbol{{check}}\leftarrow{it}\:{is}\:{my}\:{error} \\ $$$${so}\:{pls}\:{ignore}... \\ $$$${editing}... \\ $$$${T}_{{r}} =\sqrt[{\mathrm{4}}]{{r}+\mathrm{1}}\:−\sqrt[{\mathrm{4}}]{{r}}\: \\ $$$${T}_{\mathrm{1}} =\sqrt[{\mathrm{4}}]{\mathrm{2}}\:−\sqrt[{\mathrm{4}}]{\mathrm{1}}\: \\ $$$${T}_{\mathrm{2}} =\sqrt[{\mathrm{4}}]{\mathrm{3}}\:−\sqrt[{\mathrm{4}}]{\mathrm{2}}\: \\ $$$$... \\ $$$$... \\ $$$${T}_{\mathrm{255}} =\sqrt[{\mathrm{4}}]{\mathrm{256}}\:−\sqrt[{\mathrm{4}}]{\mathrm{255}}\: \\ $$$${S}=\sqrt[{\mathrm{4}}]{\mathrm{256}}\:−\sqrt[{\mathrm{4}}]{\mathrm{1}}\:=\mathrm{4}−\mathrm{1}=\mathrm{3} \\ $$

Commented by JDamian last updated on 08/Mar/20

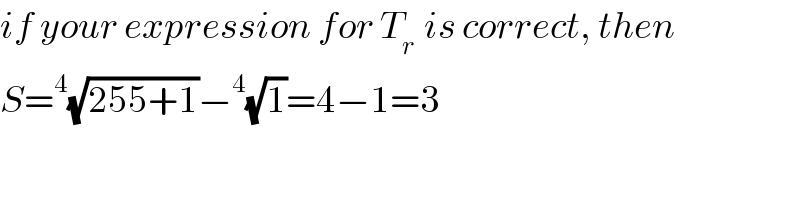
if your expression for T_(r ) is correct, then S=^4 (√(255+1))−^4 (√1)=4−1=3

$${if}\:{your}\:{expression}\:{for}\:{T}_{{r}\:} \:{is}\:{correct},\:{then} \\ $$$${S}=^{\mathrm{4}} \sqrt{\mathrm{255}+\mathrm{1}}−^{\mathrm{4}} \sqrt{\mathrm{1}}=\mathrm{4}−\mathrm{1}=\mathrm{3} \\ $$

Commented by jagoll last updated on 08/Mar/20

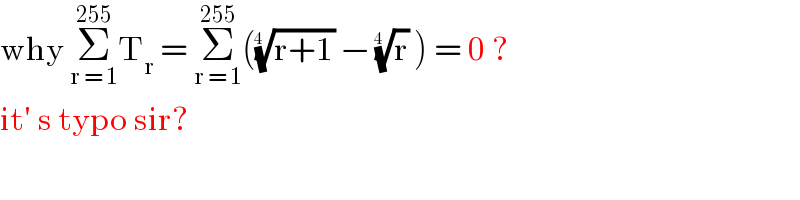
why Σ_(r = 1) ^(255) T_r = Σ_(r = 1) ^(255) (((r+1))^(1/(4 )) − (r)^(1/(4 )) ) = 0 ? it′ s typo sir?

$$\mathrm{why}\:\underset{\mathrm{r}\:=\:\mathrm{1}} {\overset{\mathrm{255}} {\sum}}\mathrm{T}_{\mathrm{r}} \:=\:\underset{\mathrm{r}\:=\:\mathrm{1}} {\overset{\mathrm{255}} {\sum}}\left(\sqrt[{\mathrm{4}\:\:}]{\mathrm{r}+\mathrm{1}}\:−\:\sqrt[{\mathrm{4}\:\:}]{\mathrm{r}}\:\right)\:=\:\mathrm{0}\:? \\ $$$$\mathrm{it}'\:\mathrm{s}\:\mathrm{typo}\:\mathrm{sir}? \\ $$

Commented by TANMAY PANACEA last updated on 08/Mar/20

yes hurry

$${yes}\:\:{hurry} \\ $$

Commented by john santu last updated on 08/Mar/20

thank you

$$\mathrm{thank}\:\mathrm{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com