Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 129057 by pipin last updated on 12/Jan/21

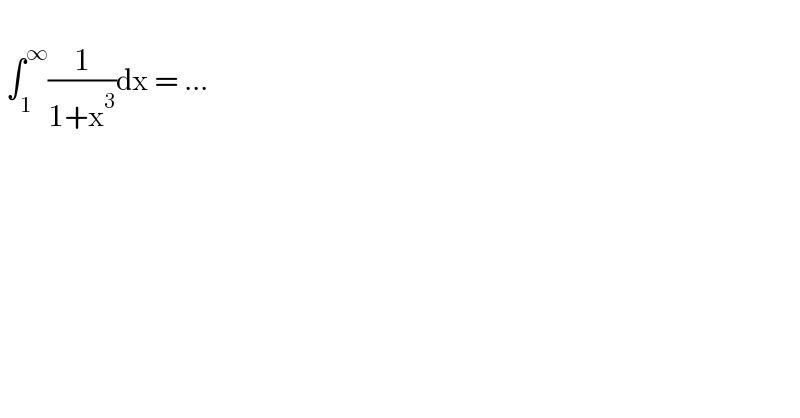
∫_1 ^∞ (1/(1+x^3 ))dx = ...

$$\: \\ $$$$\:\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{3}} }\mathrm{dx}\:=\:... \\ $$

Answered by MJS_new last updated on 12/Jan/21

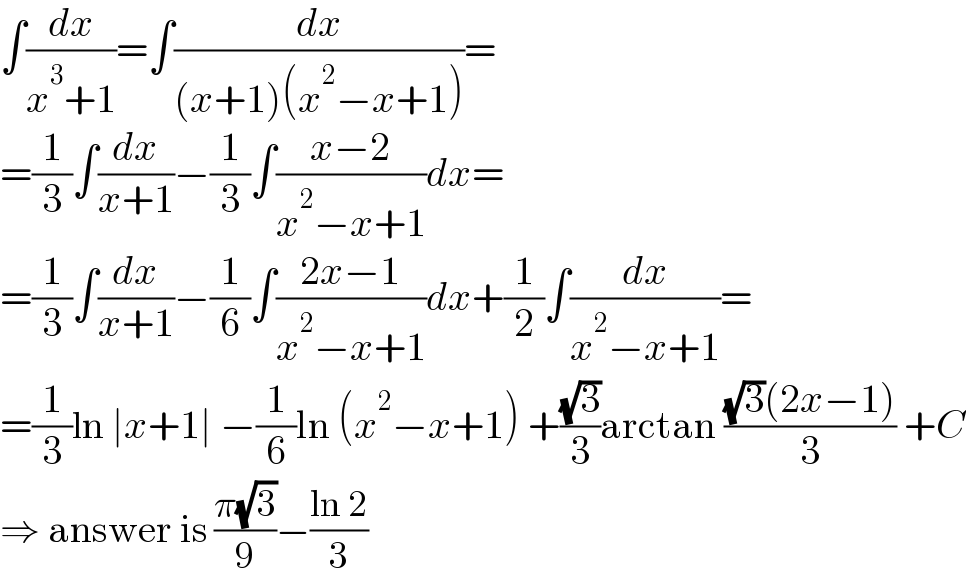
∫(dx/(x^3 +1))=∫(dx/((x+1)(x^2 −x+1)))= =(1/3)∫(dx/(x+1))−(1/3)∫((x−2)/(x^2 −x+1))dx= =(1/3)∫(dx/(x+1))−(1/6)∫((2x−1)/(x^2 −x+1))dx+(1/2)∫(dx/(x^2 −x+1))= =(1/3)ln ∣x+1∣ −(1/6)ln (x^2 −x+1) +((√3)/3)arctan (((√3)(2x−1))/3) +C ⇒ answer is ((π(√3))/9)−((ln 2)/3)

$$\int\frac{{dx}}{{x}^{\mathrm{3}} +\mathrm{1}}=\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{6}}\int\frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mid{x}+\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\:+\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{9}}−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{3}} \\ $$

Answered by Dwaipayan Shikari last updated on 12/Jan/21

∫_0 ^∞ (1/(1+x^3 ))−(1/3)∫_0 ^1 (1/(1+x))−((x−2)/(x^2 −x+1))dx =(1/3)∫_0 ^∞ (u^(−(2/3)) /(1+u))du −(1/3)∫_0 ^1 (1/(1+x))+(1/6)∫_0 ^1 ((2x−1)/(x^2 −x+1))−(1/2)∫(1/(x^2 −x+1)) =(1/3).(π/(sin((π/3))))−(1/3)log(2)−(1/( (√3)))[tan^(−1) ((2x−1)/( (√3)))]_0 ^1 =((2π)/(3(√3)))−(1/3)log(2)−(π/( 3(√3)))=(π/( 3(√3)))−(1/3)log(2)

$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}−\frac{{x}−\mathrm{2}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\frac{\mathrm{2}}{\mathrm{3}}} }{\mathrm{1}+{u}}{du}\:−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}+\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\pi}{{sin}\left(\frac{\pi}{\mathrm{3}}\right)}−\frac{\mathrm{1}}{\mathrm{3}}{log}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\left[{tan}^{−\mathrm{1}} \frac{\mathrm{2}{x}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{2}\pi}{\mathrm{3}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{3}}{log}\left(\mathrm{2}\right)−\frac{\pi}{\:\mathrm{3}\sqrt{\mathrm{3}}}=\frac{\pi}{\:\mathrm{3}\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\mathrm{3}}{log}\left(\mathrm{2}\right) \\ $$

Commented by MJS_new last updated on 12/Jan/21

I had misread the lower border...

$$\mathrm{I}\:\mathrm{had}\:\mathrm{misread}\:\mathrm{the}\:\mathrm{lower}\:\mathrm{border}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com