Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 196066 by sniper237 last updated on 17/Aug/23

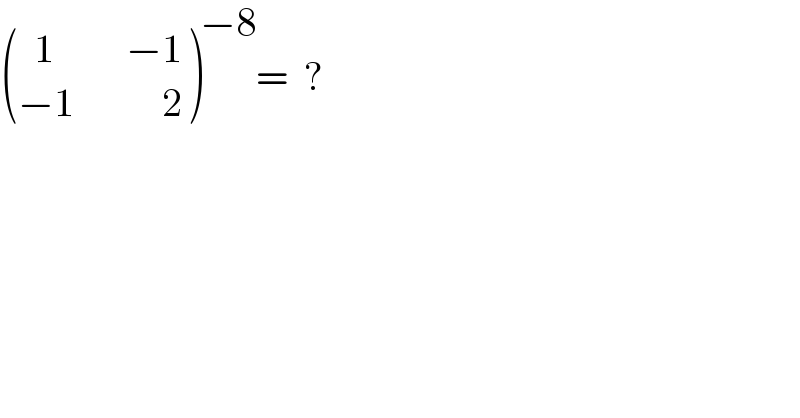
((( 1 −1)),((−1 2)) )^(−8) = ?

$$\begin{pmatrix}{\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}^{−\mathrm{8}} =\:\:? \\ $$

Answered by witcher3 last updated on 17/Aug/23

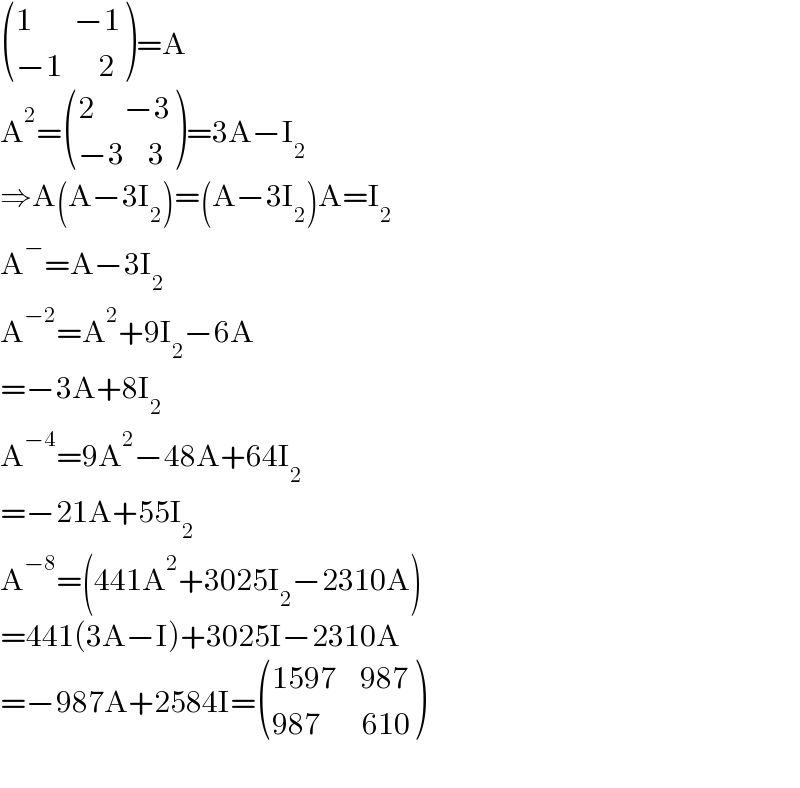
(((1 −1)),((−1 2)) )=A A^2 = (((2 −3)),((−3 3)) )=3A−I_2 ⇒A(A−3I_2 )=(A−3I_2 )A=I_2 A^− =A−3I_2 A^(−2) =A^2 +9I_2 −6A =−3A+8I_2 A^(−4) =9A^2 −48A+64I_2 =−21A+55I_2 A^(−8) =(441A^2 +3025I_2 −2310A) =441(3A−I)+3025I−2310A =−987A+2584I= (((1597 987)),((987 610)) )

$$\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}=\mathrm{A} \\ $$$$\mathrm{A}^{\mathrm{2}} =\begin{pmatrix}{\mathrm{2}\:\:\:\:\:−\mathrm{3}}\\{−\mathrm{3}\:\:\:\:\mathrm{3}}\end{pmatrix}=\mathrm{3A}−\mathrm{I}_{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{A}\left(\mathrm{A}−\mathrm{3I}_{\mathrm{2}} \right)=\left(\mathrm{A}−\mathrm{3I}_{\mathrm{2}} \right)\mathrm{A}=\mathrm{I}_{\mathrm{2}} \\ $$$$\mathrm{A}^{−} =\mathrm{A}−\mathrm{3I}_{\mathrm{2}} \\ $$$$\mathrm{A}^{−\mathrm{2}} =\mathrm{A}^{\mathrm{2}} +\mathrm{9I}_{\mathrm{2}} −\mathrm{6A} \\ $$$$=−\mathrm{3A}+\mathrm{8I}_{\mathrm{2}} \\ $$$$\mathrm{A}^{−\mathrm{4}} =\mathrm{9A}^{\mathrm{2}} −\mathrm{48A}+\mathrm{64I}_{\mathrm{2}} \\ $$$$=−\mathrm{21A}+\mathrm{55I}_{\mathrm{2}} \\ $$$$\mathrm{A}^{−\mathrm{8}} =\left(\mathrm{441A}^{\mathrm{2}} +\mathrm{3025I}_{\mathrm{2}} −\mathrm{2310A}\right) \\ $$$$=\mathrm{441}\left(\mathrm{3A}−\mathrm{I}\right)+\mathrm{3025I}−\mathrm{2310A} \\ $$$$=−\mathrm{987A}+\mathrm{2584I}=\begin{pmatrix}{\mathrm{1597}\:\:\:\:\mathrm{987}}\\{\mathrm{987}\:\:\:\:\:\:\:\mathrm{610}}\end{pmatrix} \\ $$$$ \\ $$

Answered by dimentri last updated on 18/Aug/23

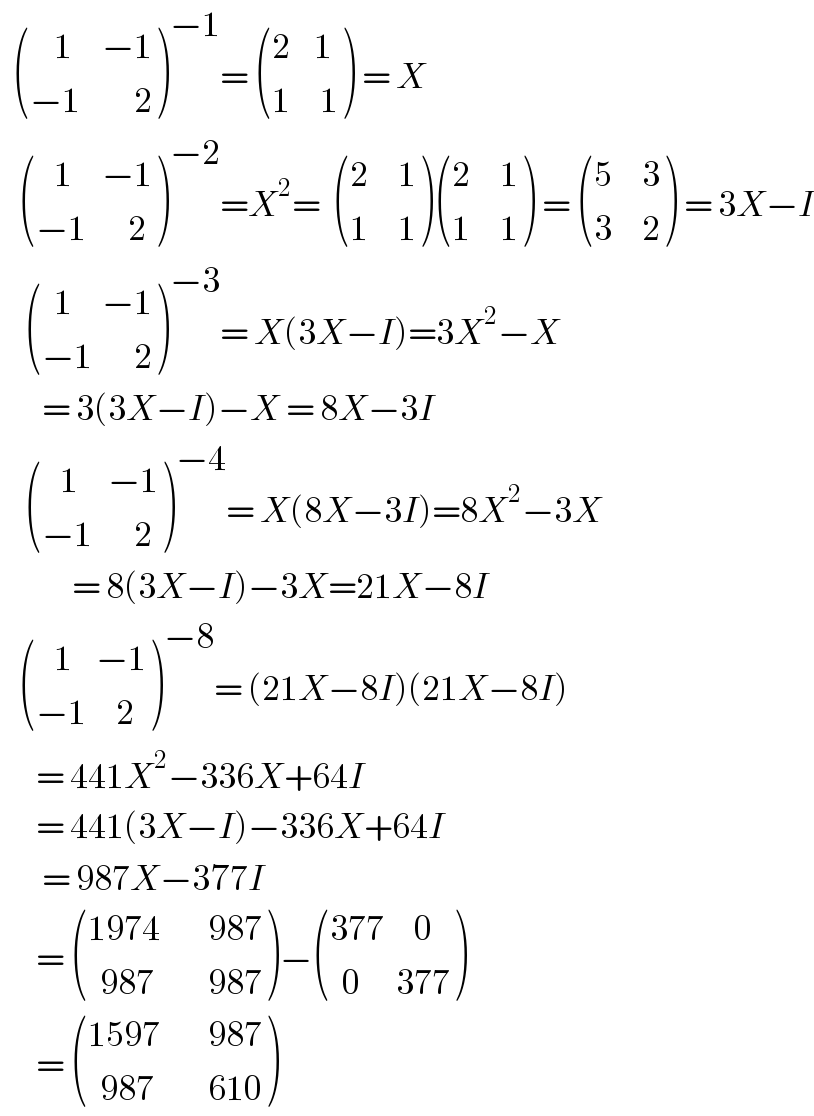
((( 1 −1)),((−1 2)) )^(−1) = (((2 1)),((1 1)) ) = X ((( 1 −1)),((−1 2)) )^(−2) =X^2 = (((2 1)),((1 1)) ) (((2 1)),((1 1)) ) = (((5 3)),((3 2)) ) = 3X−I ((( 1 −1)),((−1 2)) )^(−3) = X(3X−I)=3X^2 −X = 3(3X−I)−X = 8X−3I ((( 1 −1)),((−1 2)) )^(−4) = X(8X−3I)=8X^2 −3X = 8(3X−I)−3X=21X−8I ((( 1 −1)),((−1 2)) )^(−8) = (21X−8I)(21X−8I) = 441X^2 −336X+64I = 441(3X−I)−336X+64I = 987X−377I = (((1974 987)),(( 987 987)) )− (((377 0)),(( 0 377)) ) = (((1597 987)),(( 987 610)) )

$$\:\:\begin{pmatrix}{\:\:\:\:\mathrm{1}\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}^{−\mathrm{1}} =\:\begin{pmatrix}{\mathrm{2}\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:=\:{X} \\ $$$$\:\:\:\begin{pmatrix}{\:\:\:\mathrm{1}\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}^{−\mathrm{2}} ={X}^{\mathrm{2}} =\:\:\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\mathrm{1}}\end{pmatrix}\begin{pmatrix}{\mathrm{2}\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\mathrm{1}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{5}\:\:\:\:\:\mathrm{3}}\\{\mathrm{3}\:\:\:\:\:\mathrm{2}}\end{pmatrix}\:=\:\mathrm{3}{X}−{I} \\ $$$$\:\:\:\:\begin{pmatrix}{\:\:\mathrm{1}\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}^{−\mathrm{3}} =\:{X}\left(\mathrm{3}{X}−{I}\right)=\mathrm{3}{X}^{\mathrm{2}} −{X} \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{3}\left(\mathrm{3}{X}−{I}\right)−{X}\:=\:\mathrm{8}{X}−\mathrm{3}{I} \\ $$$$\:\:\:\:\begin{pmatrix}{\:\:\:\mathrm{1}\:\:\:\:\:−\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}}\end{pmatrix}^{−\mathrm{4}} =\:{X}\left(\mathrm{8}{X}−\mathrm{3}{I}\right)=\mathrm{8}{X}^{\mathrm{2}} −\mathrm{3}{X} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{8}\left(\mathrm{3}{X}−{I}\right)−\mathrm{3}{X}=\mathrm{21}{X}−\mathrm{8}{I} \\ $$$$\:\:\:\begin{pmatrix}{\:\:\:\mathrm{1}\:\:\:\:−\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\mathrm{2}}\end{pmatrix}^{−\mathrm{8}} =\:\left(\mathrm{21}{X}−\mathrm{8}{I}\right)\left(\mathrm{21}{X}−\mathrm{8}{I}\right) \\ $$$$\:\:\:\:\:\:=\:\mathrm{441}{X}^{\mathrm{2}} −\mathrm{336}{X}+\mathrm{64}{I} \\ $$$$\:\:\:\:\:\:=\:\mathrm{441}\left(\mathrm{3}{X}−{I}\right)−\mathrm{336}{X}+\mathrm{64}{I} \\ $$$$\:\:\:\:\:\:\:=\:\mathrm{987}{X}−\mathrm{377}{I} \\ $$$$\:\:\:\:\:\:=\:\begin{pmatrix}{\mathrm{1974}\:\:\:\:\:\:\:\:\mathrm{987}}\\{\:\:\mathrm{987}\:\:\:\:\:\:\:\:\:\mathrm{987}}\end{pmatrix}−\begin{pmatrix}{\mathrm{377}\:\:\:\:\:\mathrm{0}}\\{\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{377}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:=\:\begin{pmatrix}{\mathrm{1597}\:\:\:\:\:\:\:\:\mathrm{987}}\\{\:\:\mathrm{987}\:\:\:\:\:\:\:\:\:\mathrm{610}}\end{pmatrix}\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com