Question and Answers Forum

All Questions      Topic List

Others Questions

Previous in All Question      Next in All Question      

Previous in Others      Next in Others      

Question Number 122960 by Dwaipayan Shikari last updated on 21/Nov/20

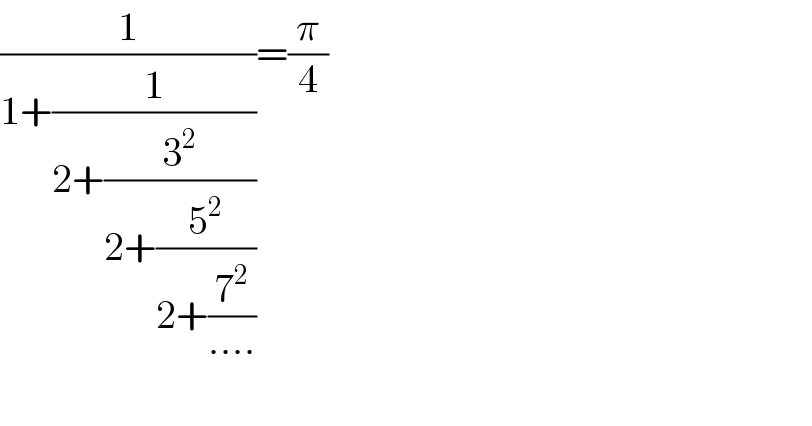
(1/(1+(1/(2+(3^2 /(2+(5^2 /(2+(7^2 /(....))))))))))=(π/4)

$$\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{7}^{\mathrm{2}} }{....}}}}}=\frac{\pi}{\mathrm{4}}\:\: \\ $$$$ \\ $$

Commented by rs4089 last updated on 21/Nov/20

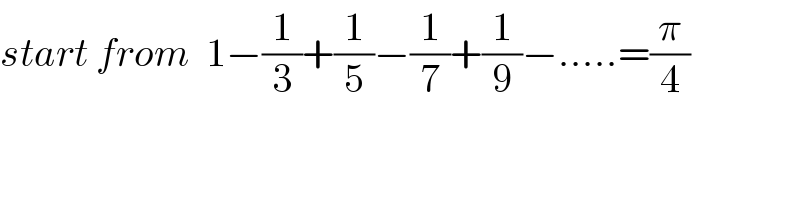
start from 1−(1/3)+(1/5)−(1/7)+(1/9)−.....=(π/4)

$${start}\:{from}\:\:\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}−.....=\frac{\pi}{\mathrm{4}} \\ $$

Commented by Dwaipayan Shikari last updated on 21/Nov/20

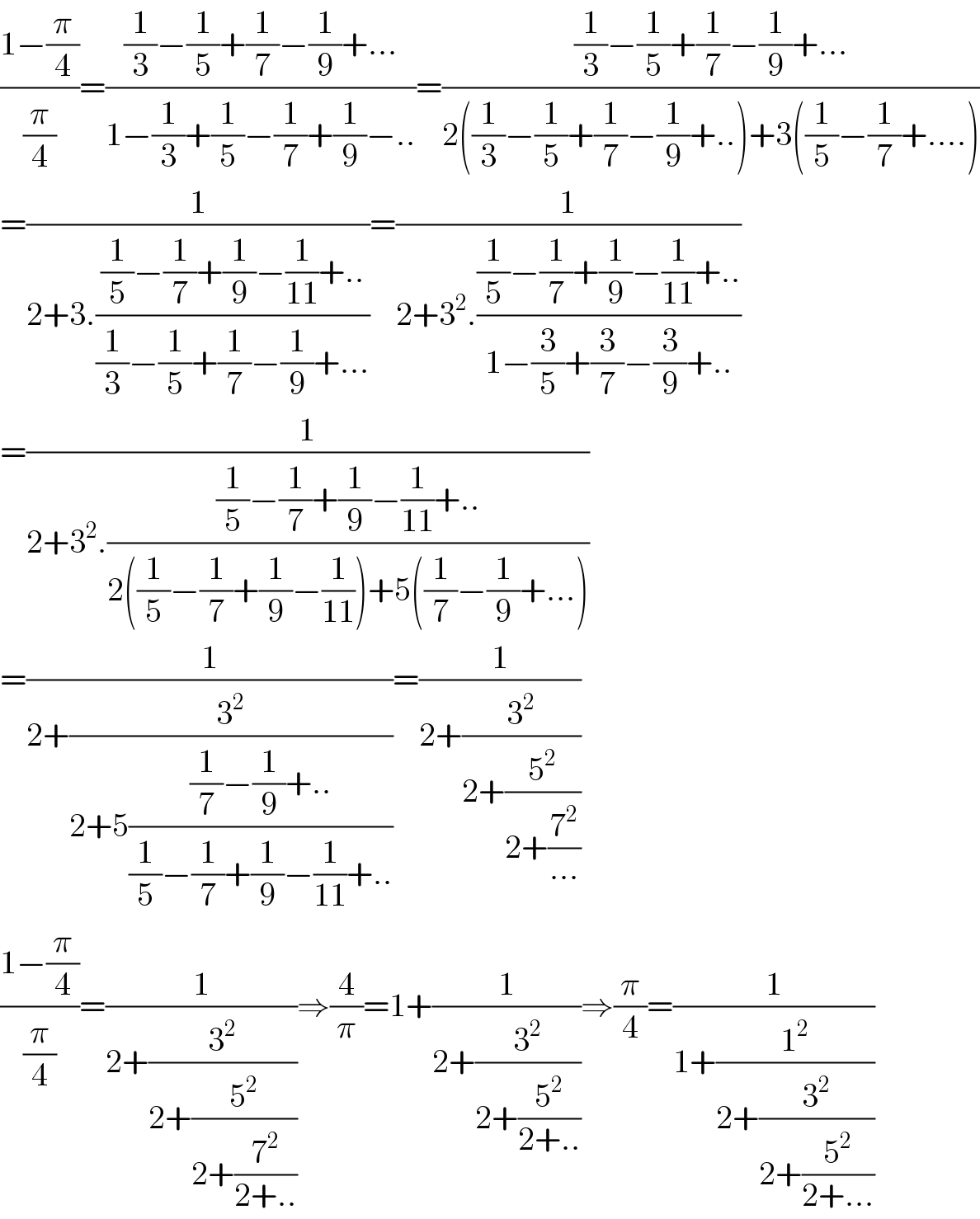
((1−(π/4))/(π/4))=(((1/3)−(1/5)+(1/7)−(1/9)+...)/(1−(1/3)+(1/5)−(1/7)+(1/9)−..))=(((1/3)−(1/5)+(1/7)−(1/9)+...)/(2((1/3)−(1/5)+(1/7)−(1/9)+..)+3((1/5)−(1/7)+....))) =(1/(2+3.(((1/5)−(1/7)+(1/9)−(1/(11))+..)/((1/3)−(1/5)+(1/7)−(1/9)+...))))=(1/(2+3^2 .(((1/5)−(1/7)+(1/9)−(1/(11))+..)/(1−(3/5)+(3/7)−(3/9)+..)))) =(1/(2+3^2 .(((1/5)−(1/7)+(1/9)−(1/(11))+..)/(2((1/5)−(1/7)+(1/9)−(1/(11)))+5((1/7)−(1/9)+...))))) =(1/(2+(3^2 /(2+5(((1/7)−(1/9)+..)/((1/5)−(1/7)+(1/9)−(1/(11))+..))))))=(1/(2+(3^2 /(2+(5^2 /(2+(7^2 /(...)))))))) ((1−(π/4))/(π/4))=(1/(2+(3^2 /(2+(5^2 /(2+(7^2 /(2+..))))))))⇒(4/π)=1+(1/(2+(3^2 /(2+(5^2 /(2+..))))))⇒(π/4)=(1/(1+(1^2 /(2+(3^2 /(2+(5^2 /(2+...))))))))

$$\frac{\mathrm{1}−\frac{\pi}{\mathrm{4}}}{\frac{\pi}{\mathrm{4}}}=\frac{\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{9}}+...}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}−..}=\frac{\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{9}}+...}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{9}}+..\right)+\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+....\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}+\mathrm{3}.\frac{\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{11}}+..}{\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{9}}+...}}=\frac{\mathrm{1}}{\mathrm{2}+\mathrm{3}^{\mathrm{2}} .\frac{\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{11}}+..}{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}}+\frac{\mathrm{3}}{\mathrm{7}}−\frac{\mathrm{3}}{\mathrm{9}}+..}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}+\mathrm{3}^{\mathrm{2}} .\frac{\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{11}}+..}{\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{11}}\right)+\mathrm{5}\left(\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{9}}+...\right)}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}+\mathrm{5}\frac{\frac{\mathrm{1}}{\mathrm{7}}−\frac{\mathrm{1}}{\mathrm{9}}+..}{\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\frac{\mathrm{1}}{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{11}}+..}}}=\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{7}^{\mathrm{2}} }{...}}}} \\ $$$$\frac{\mathrm{1}−\frac{\pi}{\mathrm{4}}}{\frac{\pi}{\mathrm{4}}}=\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{7}^{\mathrm{2}} }{\mathrm{2}+..}}}}\Rightarrow\frac{\mathrm{4}}{\pi}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}+..}}}\Rightarrow\frac{\pi}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{1}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}+\frac{\mathrm{5}^{\mathrm{2}} }{\mathrm{2}+...}}}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com