
Question Number 213844 by universe last updated on 18/Nov/24
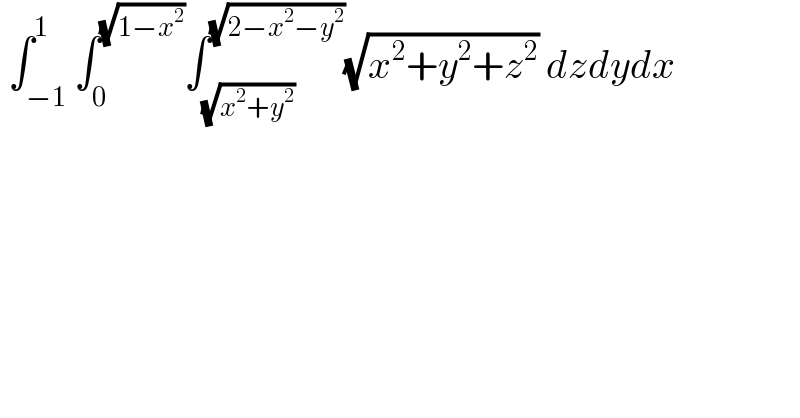
$$\:\int_{−\mathrm{1}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \int_{\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }} ^{\sqrt{\mathrm{2}−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }} \sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} }\:{dzdydx} \\ $$
Answered by BHOOPENDRA last updated on 19/Nov/24
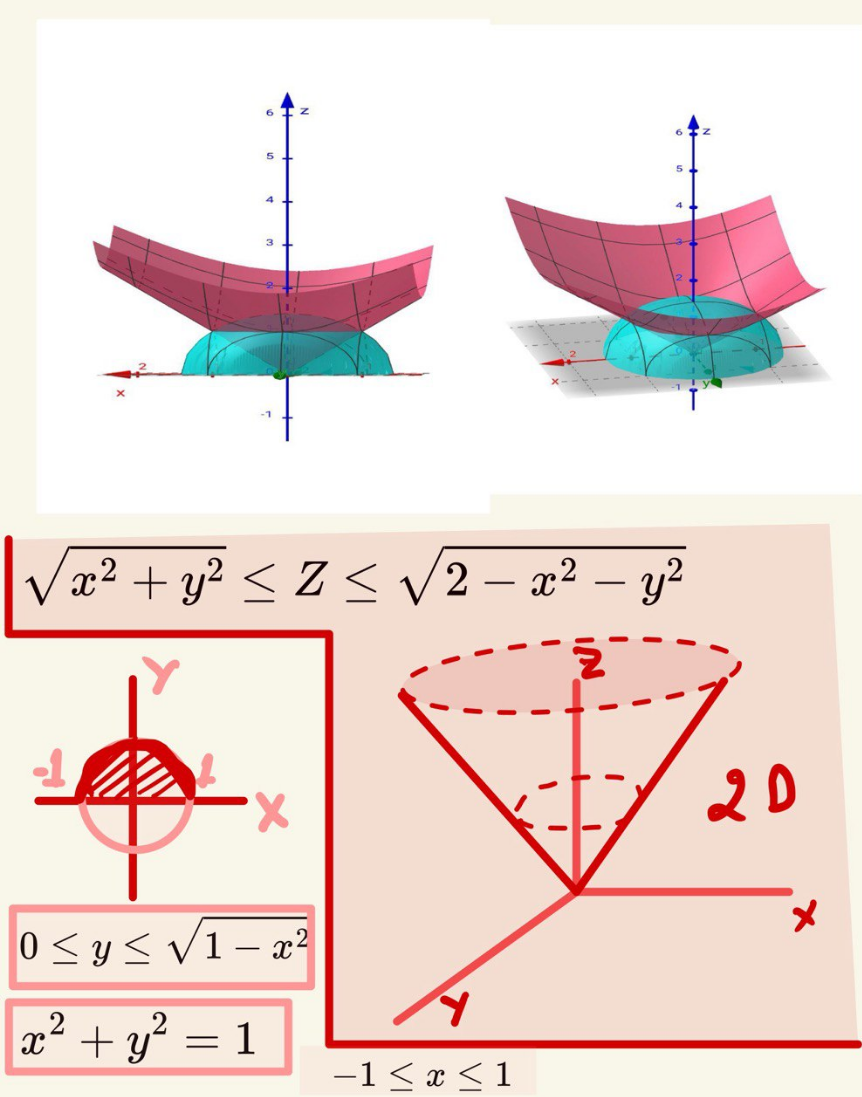
Answered by BHOOPENDRA last updated on 19/Nov/24
![Conversion of spherical coordinates x=ρsin φcos θ y=ρsin φsin θ z=ρcos φ (√(x^2 +y^2 +z^2 ))=ρ(distance from the origin) Integration bound x ranges from −1 to 1 this corresponds to θ θ∈[0,π] φ∈[0,(π/4)] ρ∈[0,(√2)] ∫_(φ=0) ^(φ=(π/4)) ∫_(θ=0) ^π ∫_(ρ=0) ^(√2) ρ. ρ^2 sin φdρdφdθ. [(ρ^4 /4)]_0 ^(√2) [−cos φ]_0 ^(π/4) [θ]_0 ^π =1.[−(1/( (√2)))+1].π =[((((√2)−1))/( (√2)))].π](Q213857.png)
$${Conversion}\:{of}\:{spherical}\:{coordinates} \\ $$$${x}=\rho\mathrm{sin}\:\phi\mathrm{cos}\:\theta \\ $$$${y}=\rho\mathrm{sin}\:\phi\mathrm{sin}\:\theta \\ $$$${z}=\rho\mathrm{cos}\:\phi \\ $$$$\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \:}=\rho\left({distance}\:{from}\:{the}\:{origin}\right) \\ $$$$ \\ $$$${Integration}\:{bound} \\ $$$${x}\:{ranges}\:{from}\:−\mathrm{1}\:{to}\:\mathrm{1} \\ $$$${this}\:{corresponds}\:{to}\:\theta\: \\ $$$$\theta\in\left[\mathrm{0},\pi\right] \\ $$$$\phi\in\left[\mathrm{0},\frac{\pi}{\mathrm{4}}\right] \\ $$$$\rho\in\left[\mathrm{0},\sqrt{\mathrm{2}}\right] \\ $$$$\int_{\phi=\mathrm{0}} ^{\phi=\frac{\pi}{\mathrm{4}}} \:\int_{\theta=\mathrm{0}} ^{\pi} \int_{\rho=\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\:\rho.\:\:\rho^{\mathrm{2}} \mathrm{sin}\:\phi{d}\rho{d}\phi{d}\theta. \\ $$$$\left[\frac{\rho^{\mathrm{4}} }{\mathrm{4}}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\left[−\mathrm{cos}\:\phi\right]_{\mathrm{0}} ^{\pi/\mathrm{4}} \:\left[\theta\right]_{\mathrm{0}} ^{\pi} \\ $$$$=\mathrm{1}.\left[−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\mathrm{1}\right].\pi \\ $$$$=\left[\frac{\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\:\sqrt{\mathrm{2}}}\right].\pi \\ $$
Answered by BHOOPENDRA last updated on 19/Nov/24
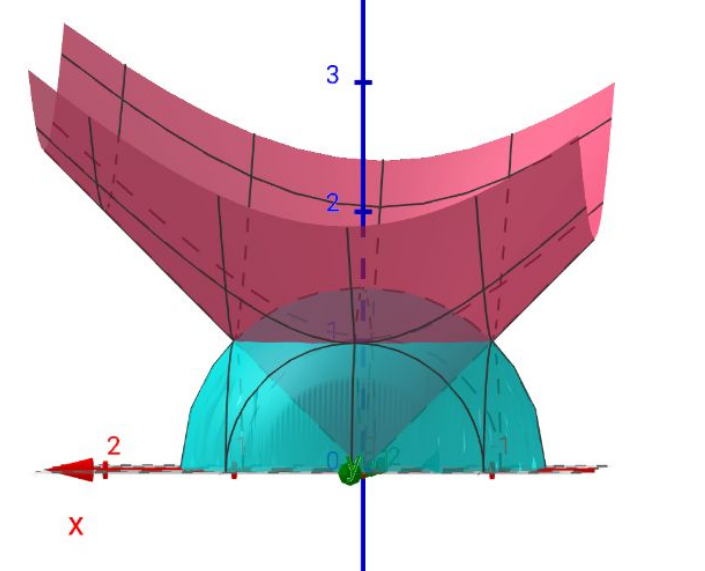
Commented by universe last updated on 19/Nov/24
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
