
Question Number 171611 by Gbenga last updated on 18/Jun/22
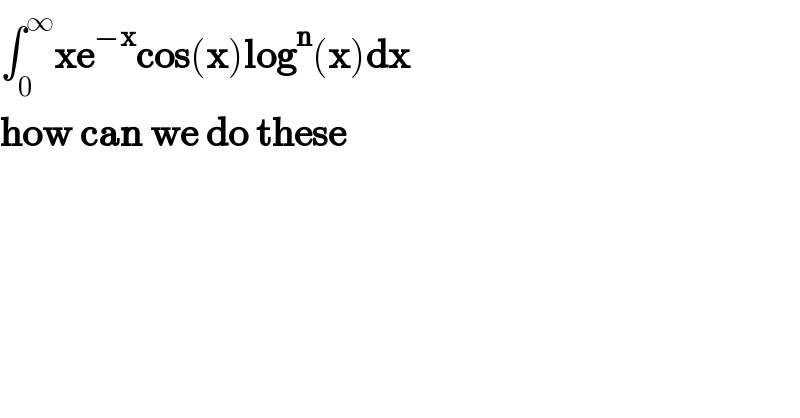
$$\int_{\mathrm{0}} ^{\infty} \boldsymbol{\mathrm{xe}}^{−\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{log}}^{\boldsymbol{\mathrm{n}}} \left(\boldsymbol{\mathrm{x}}\right)\boldsymbol{\mathrm{dx}} \\ $$$$\boldsymbol{\mathrm{how}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{we}}\:\boldsymbol{\mathrm{do}}\:\boldsymbol{\mathrm{these}} \\ $$
Answered by mindispower last updated on 19/Jun/22

$$={Re}\int_{\mathrm{0}} ^{\infty} {xe}^{−{x}\left(\mathrm{1}+{i}\right)} {ln}^{{n}} \left({x}\right){dx} \\ $$$${Re}\left({e}^{−{ix}} \right)={cos}\left({x}\right).... \\ $$$${ln}\left({x}\right)=\frac{{d}}{{da}}{x}^{{a}} \mid_{{a}=\mathrm{0}} \\ $$$${let}\:{I}_{{n}} ={Our}\:{Integral} \\ $$$${I}_{{n}} =\frac{{d}^{{n}} }{{da}^{{n}} }{Re}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{1}+{a}} {e}^{−{x}\left(\mathrm{1}+{i}\right)} {dx}\mid_{{a}=\mathrm{0}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{1}+{a}} {e}^{−{x}\left(\mathrm{1}+{i}\right)} {dx}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{i}\right)^{{a}} }{u}^{\mathrm{1}+{a}} {e}^{−{u}} {du} \\ $$$$=\frac{\Gamma\left(\mathrm{2}+{a}\right)}{\left(\mathrm{1}+{i}\right)^{{a}+\mathrm{2}} } \\ $$$${I}_{{n}} =\frac{{d}^{{n}} }{{da}^{{n}} }\Gamma\left(\mathrm{2}+{a}\right){Re}\left(\mathrm{1}+{i}\right)^{−{a}−\mathrm{2}} \\ $$$$=\frac{{d}^{{n}} }{{da}^{{n}} }\Gamma\left(\mathrm{2}+{a}\right){Re}\left({e}^{−\left({a}+\mathrm{2}\right){ln}\left(\sqrt{\mathrm{2}}\right).} {e}^{−\left({a}+\mathrm{2}\right)\left(\frac{{i}\pi}{\mathrm{4}}\right){p}} \right) \\ $$$$={Re}\left\{\frac{{d}^{{n}} }{{da}^{{n}} }\Gamma\left(\mathrm{2}+{a}\right){e}^{\left({a}+\mathrm{2}\right)\left(−\frac{{i}\pi}{\mathrm{4}}−{ln}\left(\sqrt{\mathrm{2}}\right)\right)} \right\}_{{a}=\mathrm{0}} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\Gamma^{\left({n}−{k}\right)} \left(\mathrm{2}+{a}\right)\left({e}^{\left({a}+\mathrm{2}\right)\left(−\frac{{i}\pi}{\mathrm{4}}−{ln}\left(\sqrt{\mathrm{2}}\right)\right)} \right)^{\left({k}\right)} \mid_{{a}=\mathrm{0}} \\ $$$${f}^{\left({k}\right)} .{k}\:{th}\:{Derivat}\:{of}\:{f}...{f}^{\left(\mathrm{0}\right)} ={f} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\Gamma^{\left({n}−{k}\right)} \left(\mathrm{2}\right).\left(\left(−{i}\frac{\pi}{\mathrm{4}}−{ln}\left(\sqrt{\mathrm{2}}\right)\right)\right)^{\left({k}\right)} {e}^{\left({a}+\mathrm{2}\right)\left(−\frac{{i}\pi}{\mathrm{4}}−{ln}\left(\sqrt{\mathrm{2}}\right)\right)} \\ $$$$−{ln}\left(\sqrt{\mathrm{2}}\right)+\frac{\mathrm{i}\pi}{\mathrm{4}}=\sqrt{\left({ln}\left(\sqrt{\mathrm{2}}\right)\right)^{\mathrm{2}} +\frac{\pi^{\mathrm{2}} }{\mathrm{16}}}{e}^{{i}\left(\pi+{arctan}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\pi\right)\right)} ={re}^{{is}} \\ $$$${I}_{{n}} ={Re}\left\{\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\Gamma^{\left({n}−{k}\right)} \left(\mathrm{2}\right){r}^{{k}} {e}^{{iks}} {e}^{−\frac{{i}\pi}{\mathrm{2}}−\mathrm{2}{ln}\left(\sqrt{\mathrm{2}}\right)} \right\} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\Gamma^{\left({n}−{k}\right)} \left(\mathrm{2}\right){r}^{{k}} {cos}\left({ks}−\frac{{i}\pi}{\mathrm{2}}−\mathrm{2}{ln}\left(\sqrt{\mathrm{2}}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\Gamma^{\left({n}−{k}\right)} \left(\mathrm{2}\right){r}^{{k}} {cos}\left({k}\left(\pi+\mathrm{tan}^{−\mathrm{1}} \left(\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\pi\right)−\frac{\pi}{\mathrm{2}}\right)\right)\right) \\ $$$$ \\ $$$$ \\ $$
Commented by Gbenga last updated on 20/Jun/22

$$\boldsymbol{\mathrm{thanks}}\:\boldsymbol{\mathrm{Sir}} \\ $$
