
Question Number 74264 by malikmasood3535@gmail.com last updated on 21/Nov/19
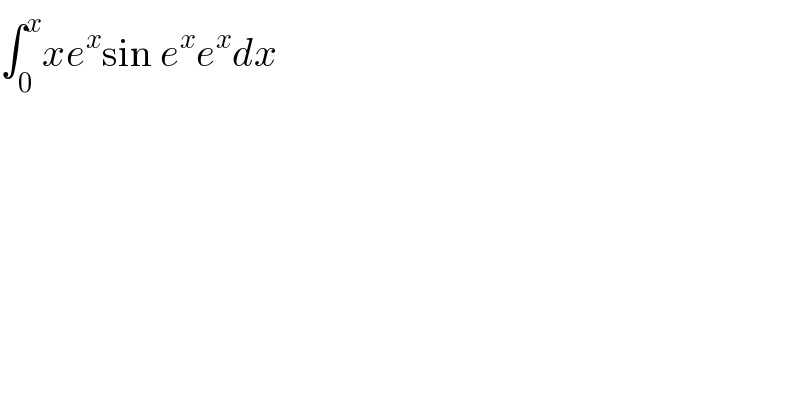
$$\int_{\mathrm{0}} ^{{x}} {xe}^{{x}} \mathrm{sin}\:{e}^{{x}} {e}^{{x}} {dx} \\ $$
Commented by MJS last updated on 21/Nov/19

$$\left(\mathrm{1}\right)\:\mathrm{dependent}\:\mathrm{borders}\:\mathrm{error} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:{x}\mathrm{e}^{{x}} \mathrm{sin}\:\left(\mathrm{e}^{{x}} \mathrm{e}^{{x}} \right)\:={x}\mathrm{e}^{{x}} \mathrm{sin}\:\mathrm{e}^{\mathrm{2}{x}} ? \\ $$$$ \\ $$$$\mathrm{same}\:\mathrm{problems}\:\mathrm{with}\:\mathrm{the}\:\mathrm{cosinus}−\mathrm{question} \\ $$
