Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 145081 by qaz last updated on 02/Jul/21

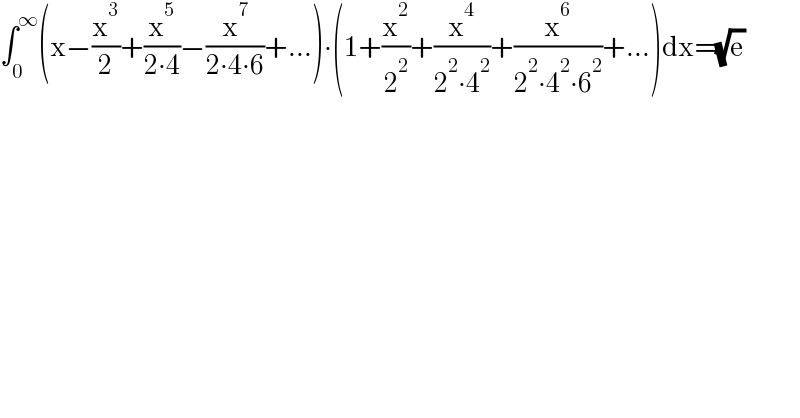
∫_0 ^∞ (x−(x^3 /2)+(x^5 /(2∙4))−(x^7 /(2∙4∙6))+...)∙(1+(x^2 /2^2 )+(x^4 /(2^2 ∙4^2 ))+(x^6 /(2^2 ∙4^2 ∙6^2 ))+...)dx=(√e)

$$\int_{\mathrm{0}} ^{\infty} \left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{2}\centerdot\mathrm{4}}−\frac{\mathrm{x}^{\mathrm{7}} }{\mathrm{2}\centerdot\mathrm{4}\centerdot\mathrm{6}}+...\right)\centerdot\left(\mathrm{1}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{4}^{\mathrm{2}} }+\frac{\mathrm{x}^{\mathrm{6}} }{\mathrm{2}^{\mathrm{2}} \centerdot\mathrm{4}^{\mathrm{2}} \centerdot\mathrm{6}^{\mathrm{2}} }+...\right)\mathrm{dx}=\sqrt{\mathrm{e}} \\ $$

Answered by mindispower last updated on 02/Jul/21

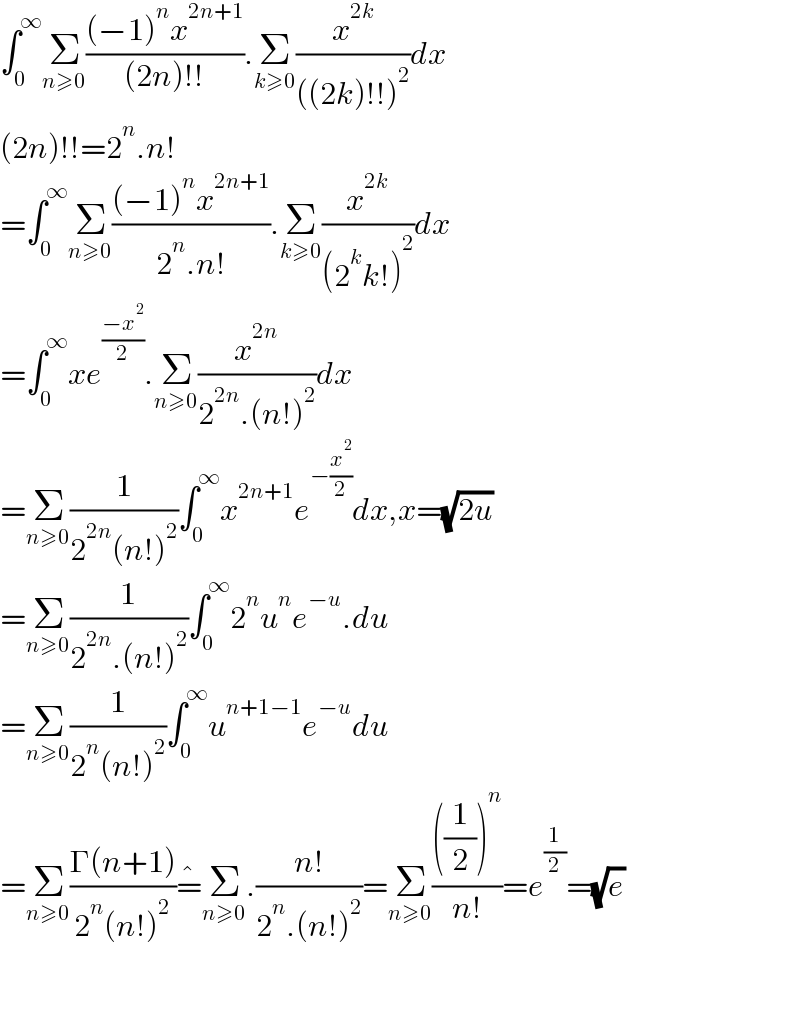
∫_0 ^∞ Σ_(n≥0) (((−1)^n x^(2n+1) )/((2n)!!)).Σ_(k≥0) (x^(2k) /(((2k)!!)^2 ))dx (2n)!!=2^n .n! =∫_0 ^∞ Σ_(n≥0) (((−1)^n x^(2n+1) )/(2^n .n!)).Σ_(k≥0) (x^(2k) /((2^k k!)^2 ))dx =∫_0 ^∞ xe^((−x^2 )/2) .Σ_(n≥0) (x^(2n) /(2^(2n) .(n!)^2 ))dx =Σ_(n≥0) (1/(2^(2n) (n!)^2 ))∫_0 ^∞ x^(2n+1) e^(−(x^2 /2)) dx,x=(√(2u)) =Σ_(n≥0) (1/(2^(2n) .(n!)^2 ))∫_0 ^∞ 2^n u^n e^(−u) .du =Σ_(n≥0) (1/(2^n (n!)^2 ))∫_0 ^∞ u^(n+1−1) e^(−u) du =Σ_(n≥0) ((Γ(n+1))/(2^n (n!)^2 ))=^� Σ_(n≥0) .((n!)/(2^n .(n!)^2 ))=Σ_(n≥0) ((((1/2))^n )/(n!))=e^(1/2) =(√e)

$$\int_{\mathrm{0}} ^{\infty} \underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}\right)!!}.\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{\mathrm{2}{k}} }{\left(\left(\mathrm{2}{k}\right)!!\right)^{\mathrm{2}} }{dx} \\ $$$$\left(\mathrm{2}{n}\right)!!=\mathrm{2}^{{n}} .{n}! \\ $$$$=\int_{\mathrm{0}} ^{\infty} \underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}^{{n}} .{n}!}.\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{{x}^{\mathrm{2}{k}} }{\left(\mathrm{2}^{{k}} {k}!\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {xe}^{\frac{−{x}^{\mathrm{2}} }{\mathrm{2}}} .\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{x}^{\mathrm{2}{n}} }{\mathrm{2}^{\mathrm{2}{n}} .\left({n}!\right)^{\mathrm{2}} }{dx} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}} \left({n}!\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}{n}+\mathrm{1}} {e}^{−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {dx},{x}=\sqrt{\mathrm{2}{u}} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}{n}} .\left({n}!\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} \mathrm{2}^{{n}} {u}^{{n}} {e}^{−{u}} .{du} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\mathrm{2}^{{n}} \left({n}!\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{\infty} {u}^{{n}+\mathrm{1}−\mathrm{1}} {e}^{−{u}} {du} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\Gamma\left({n}+\mathrm{1}\right)}{\mathrm{2}^{{n}} \left({n}!\right)^{\mathrm{2}} }\hat {=}\underset{{n}\geqslant\mathrm{0}} {\sum}.\frac{{n}!}{\mathrm{2}^{{n}} .\left({n}!\right)^{\mathrm{2}} }=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} }{{n}!}={e}^{\frac{\mathrm{1}}{\mathrm{2}}} =\sqrt{{e}} \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com