
Question Number 163033 by mnjuly1970 last updated on 03/Jan/22
![Ω= ∫_0 ^( ∞) (( x − sin (x ))/x^( 3) )dx −−− solution−−− Ω=^(I.B.P) [ ((−1)/(2 x^( 2) )) (x−sin(x))]_0 ^∞ +(1/2) ∫_0 ^( ∞) ((1−cos (x))/x^( 2) )dx = (1/2) ∫_0 ^( ∞) (( 2sin^( 2) ((x/2)))/x^( 2) )dx=∫_0 ^( ∞) ((sin^( 2) ((x/2)))/x^( 2) )dx =^((x/2) = α) (1/2)∫_0 ^( ∞) ((sin^( 2) ( α))/α^( 2) ) dα = (1/2) [((−1)/α) sin^( 2) (α)]_0 ^∞ +(1/2)∫_0 ^( ∞) ((sin(2α))/α)dα =^(2α=ϕ) (1/2) ∫_0 ^( ∞) (( sin(ϕ ))/ϕ) dϕ =(π/4) −− Ω= (π/4) −−−](Q163033.png)
$$ \\ $$$$\:\:\:\:\Omega=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{x}\:−\:{sin}\:\left({x}\:\right)}{{x}^{\:\mathrm{3}} }{dx} \\ $$$$−−−\:{solution}−−− \\ $$$$\:\:\:\:\:\Omega\overset{\mathscr{I}.\mathscr{B}.\mathscr{P}} {=}\:\left[\:\frac{−\mathrm{1}}{\mathrm{2}\:{x}^{\:\mathrm{2}} }\:\left({x}−{sin}\left({x}\right)\right)\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}−{cos}\:\left({x}\right)}{{x}^{\:\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:\mathrm{2}{sin}^{\:\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{{x}^{\:\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}^{\:\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{{x}^{\:\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\overset{\frac{{x}}{\mathrm{2}}\:=\:\alpha} {=}\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}^{\:\mathrm{2}} \left(\:\alpha\right)}{\alpha^{\:\mathrm{2}} }\:{d}\alpha\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left[\frac{−\mathrm{1}}{\alpha}\:{sin}^{\:\mathrm{2}} \left(\alpha\right)\right]_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{sin}\left(\mathrm{2}\alpha\right)}{\alpha}{d}\alpha \\ $$$$\:\:\:\:\:\:\:\:\overset{\mathrm{2}\alpha=\varphi} {=}\:\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\:\infty} \frac{\:{sin}\left(\varphi\:\right)}{\varphi}\:{d}\varphi\:=\frac{\pi}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−−\:\:\:\:\:\Omega=\:\frac{\pi}{\mathrm{4}}\:\:−−− \\ $$$$ \\ $$$$ \\ $$
Answered by qaz last updated on 03/Jan/22
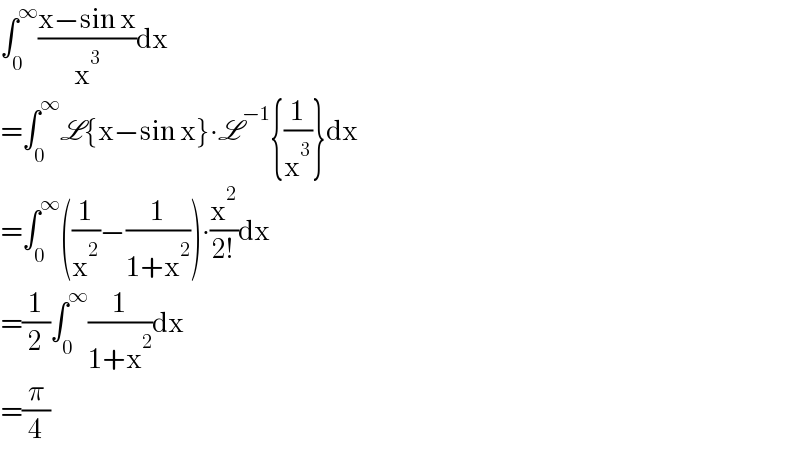
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} }\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \mathscr{L}\left\{\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right\}\centerdot\mathscr{L}^{−\mathrm{1}} \left\{\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{3}} }\right\}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\centerdot\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}!}\mathrm{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\frac{\pi}{\mathrm{4}} \\ $$
Commented by mnjuly1970 last updated on 03/Jan/22
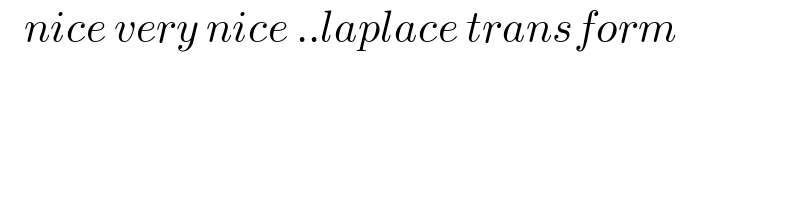
$$\:\:\:{nice}\:{very}\:{nice}\:..{laplace}\:{transform} \\ $$
