
Question Number 218599 by Nicholas666 last updated on 12/Apr/25
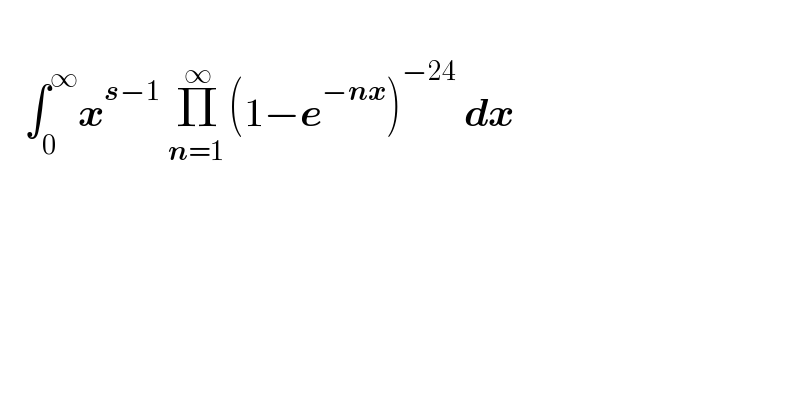
$$ \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\infty} \boldsymbol{{x}}^{\boldsymbol{{s}}−\mathrm{1}} \:\underset{\boldsymbol{{n}}=\mathrm{1}\:} {\overset{\infty} {\prod}}\left(\mathrm{1}−\boldsymbol{{e}}^{−\boldsymbol{{nx}}} \right)^{−\mathrm{24}} \:\boldsymbol{{dx}} \\ $$$$ \\ $$
Commented by MrGaster last updated on 12/Apr/25
=Γ(s)ζ(s)^(24) (2): =∫_0 ^∞ x^(s−1) (Σ_(n=1) ^∞ p(n)e^(−nx) )^(24) dx =Σ_(n=1) ^∞ p(n)^(24) ∫_0 ^∞ x^(s−1) e^(−n24x) dx =Σ_(n=1) ^∞ p(n)^(24) ((Γ(s))/((n24)^s )) =((Γ(s))/((24)^s ))Σ_(n=1) ^∞ ((p(n)^(24) )/n^s ) = determinant ((((Γ(s)ζ(s−23))/((24)^s )))) (3): =∫_0 ^∞ x^(s−1) e^x Δ(((ix)/(2π)))^(−1) dx(let τ=((ix)/(2π))) =∫_0 ^∞ x^(s−1) e^x (Σ_(m=1) ^∞ τ(m)e^(−mx) )^(−1) dx =Γ(s)Σ_(m=1) ^∞ ((τ(m))/m^s )(appy mellin transfrom) =Γ(s)∙2^(12) π^(12) ((Γ(s))/(Γ(s+12)))(corrected to modular formu L-fnction relation) =((Γ(s)Γ(s−11))/(Γ(s+1)))∙24!(using functional equation) ∫_0 ^∞ x^(s−1) Π_(n=1 ) ^∞ (1−e^(−nx) )^(−24) dx=Γ(s)Γ(s−11)ζ(s−11)](Q218600.png)
$$\mathrm{I}\:\mathrm{have}\:\mathrm{worked}\:\mathrm{out}\:\mathrm{threet} \\ $$$$\mathrm{resuls}\:\mathrm{at}\:\mathrm{hand}\:\mathrm{and}\:\mathrm{I}\:\mathrm{dontw} \\ $$$$\mathrm{kno}\:\mathrm{which}\:\mathrm{one}\:\mathrm{is}\:\mathrm{right}.\:\mathrm{Forf} \\ $$$$\mathrm{reerence}\:\mathrm{only}: \\ $$$$\left(\mathrm{1}\right): \\ $$$$=\int_{\mathrm{0}} ^{\infty} {x}^{{s}−\mathrm{1}} \eta\left(\frac{{i}}{{x}}\right)^{−\mathrm{24}} {dx} \\ $$$$\eta\left(\frac{{i}}{{x}}\right)=\sqrt{{x}}{e}^{−{i}\pi/\mathrm{4}} \eta\left({ix}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{{s}−\mathrm{1}} \left(\sqrt{{x}}{e}^{−{i}\pi/\mathrm{4}} \eta\left({ix}\right)\right)^{−\mathrm{24}} {dx} \\ $$$$\left.=\int_{\mathrm{0}} ^{\infty} {x}^{{s}−\mathrm{1}} {x}^{−\mathrm{12}} {e}^{{i}\mathrm{6}\pi} \eta\left({ix}\right)\right)^{−\mathrm{24}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {x}^{{s}−\mathrm{13}} \eta\left({ix}\right)^{−\mathrm{24}} {dx} \\ $$$$\mathcal{M}\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−{e}^{−{nx}} \right)^{−\mathrm{24}} \right]\left({s}\right)=\Gamma\left({s}\right)\zeta\left({s}\right)^{\mathrm{24}} \\ $$$$\left(\mathrm{2}\right): \\ $$$$=\int_{\mathrm{0}} ^{\infty} {x}^{{s}−\mathrm{1}} \left(\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{p}\left({n}\right){e}^{−{nx}} \right)^{\mathrm{24}} {dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{p}\left({n}\right)^{\mathrm{24}} \int_{\mathrm{0}} ^{\infty} {x}^{{s}−\mathrm{1}} {e}^{−{n}\mathrm{24}{x}} {dx} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{p}\left({n}\right)^{\mathrm{24}} \frac{\Gamma\left({s}\right)}{\left({n}\mathrm{24}\right)^{{s}} } \\ $$$$=\frac{\Gamma\left({s}\right)}{\left(\mathrm{24}\right)^{{s}} }\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{p}\left({n}\right)^{\mathrm{24}} }{{n}^{{s}} } \\ $$$$=\begin{array}{|c|}{\frac{\Gamma\left({s}\right)\zeta\left({s}−\mathrm{23}\right)}{\left(\mathrm{24}\right)^{{s}} }}\\\hline\end{array} \\ $$$$\left(\mathrm{3}\right): \\ $$$$=\int_{\mathrm{0}} ^{\infty} {x}^{{s}−\mathrm{1}} {e}^{{x}} \Delta\left(\frac{{ix}}{\mathrm{2}\pi}\right)^{−\mathrm{1}} {dx}\left(\mathrm{let}\:\tau=\frac{{ix}}{\mathrm{2}\pi}\right) \\ $$$$=\int_{\mathrm{0}} ^{\infty} {x}^{{s}−\mathrm{1}} {e}^{{x}} \left(\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\tau\left({m}\right){e}^{−{mx}} \right)^{−\mathrm{1}} {dx} \\ $$$$=\Gamma\left({s}\right)\underset{{m}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\tau\left({m}\right)}{{m}^{{s}} }\left(\mathrm{appy}\:\mathrm{mellin}\:\mathrm{transfrom}\right) \\ $$$$=\Gamma\left({s}\right)\centerdot\mathrm{2}^{\mathrm{12}} \pi^{\mathrm{12}} \frac{\Gamma\left({s}\right)}{\Gamma\left({s}+\mathrm{12}\right)}\left(\mathrm{corrected}\:\mathrm{to}\:\mathrm{modular}\:\mathrm{formu}\:\mathrm{L}-\mathrm{fnction}\:\mathrm{relation}\right) \\ $$$$=\frac{\Gamma\left({s}\right)\Gamma\left({s}−\mathrm{11}\right)}{\Gamma\left({s}+\mathrm{1}\right)}\centerdot\mathrm{24}!\left(\mathrm{using}\:\mathrm{functional}\:\mathrm{equation}\right) \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\infty} \boldsymbol{{x}}^{\boldsymbol{{s}}−\mathrm{1}} \:\underset{\boldsymbol{{n}}=\mathrm{1}\:} {\overset{\infty} {\prod}}\left(\mathrm{1}−\boldsymbol{{e}}^{−\boldsymbol{{nx}}} \right)^{−\mathrm{24}} \:\boldsymbol{{dx}}=\Gamma\left({s}\right)\Gamma\left({s}−\mathrm{11}\right)\zeta\left({s}−\mathrm{11}\right) \\ $$
Commented by Nicholas666 last updated on 16/Apr/25

$${thank}\:{you}\:{prof} \\ $$$$ \\ $$
