
Question Number 210112 by klipto last updated on 30/Jul/24
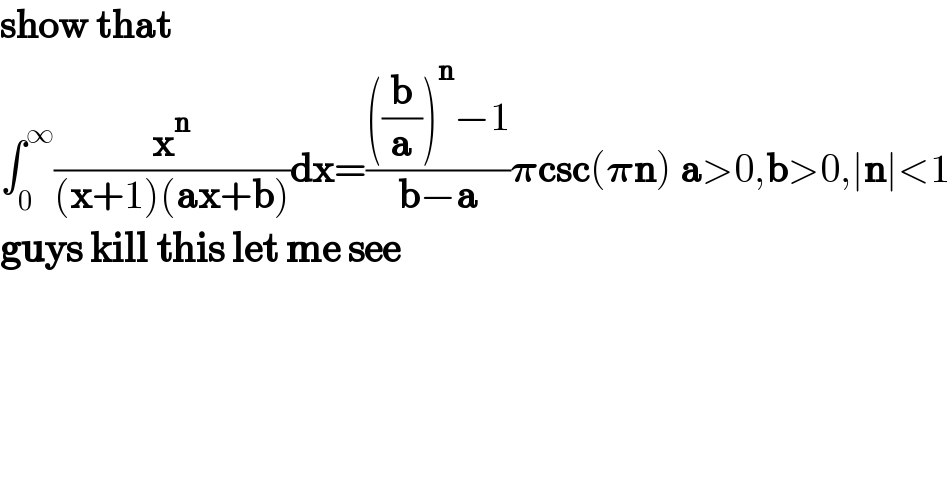
$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{\mathrm{x}}^{\boldsymbol{\mathrm{n}}} }{\left(\boldsymbol{\mathrm{x}}+\mathrm{1}\right)\left(\boldsymbol{\mathrm{ax}}+\boldsymbol{\mathrm{b}}\right)}\boldsymbol{\mathrm{dx}}=\frac{\left(\frac{\boldsymbol{\mathrm{b}}}{\boldsymbol{\mathrm{a}}}\right)^{\boldsymbol{\mathrm{n}}} −\mathrm{1}}{\boldsymbol{\mathrm{b}}−\boldsymbol{\mathrm{a}}}\boldsymbol{\pi\mathrm{csc}}\left(\boldsymbol{\pi\mathrm{n}}\right)\:\boldsymbol{\mathrm{a}}>\mathrm{0},\boldsymbol{\mathrm{b}}>\mathrm{0},\mid\boldsymbol{\mathrm{n}}\mid<\mathrm{1} \\ $$$$\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{that}} \\ $$
