
Question Number 8672 by swapnil last updated on 20/Oct/16
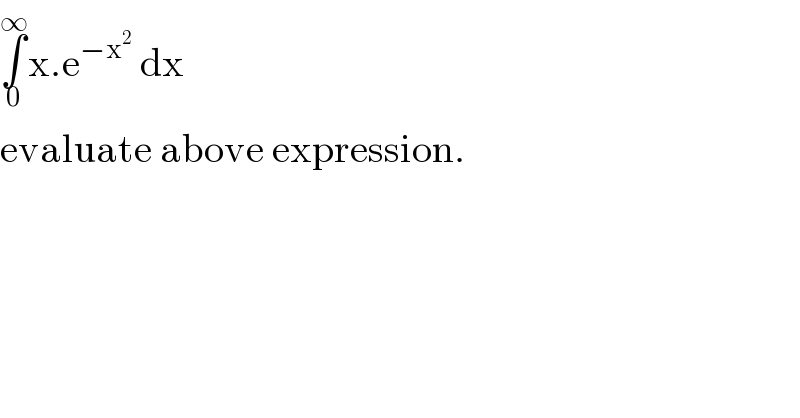
$$\underset{\mathrm{0}} {\overset{\infty} {\int}}\mathrm{x}.\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \:\mathrm{dx} \\ $$$$\mathrm{evaluate}\:\mathrm{above}\:\mathrm{expression}. \\ $$
Answered by 123456 last updated on 21/Oct/16
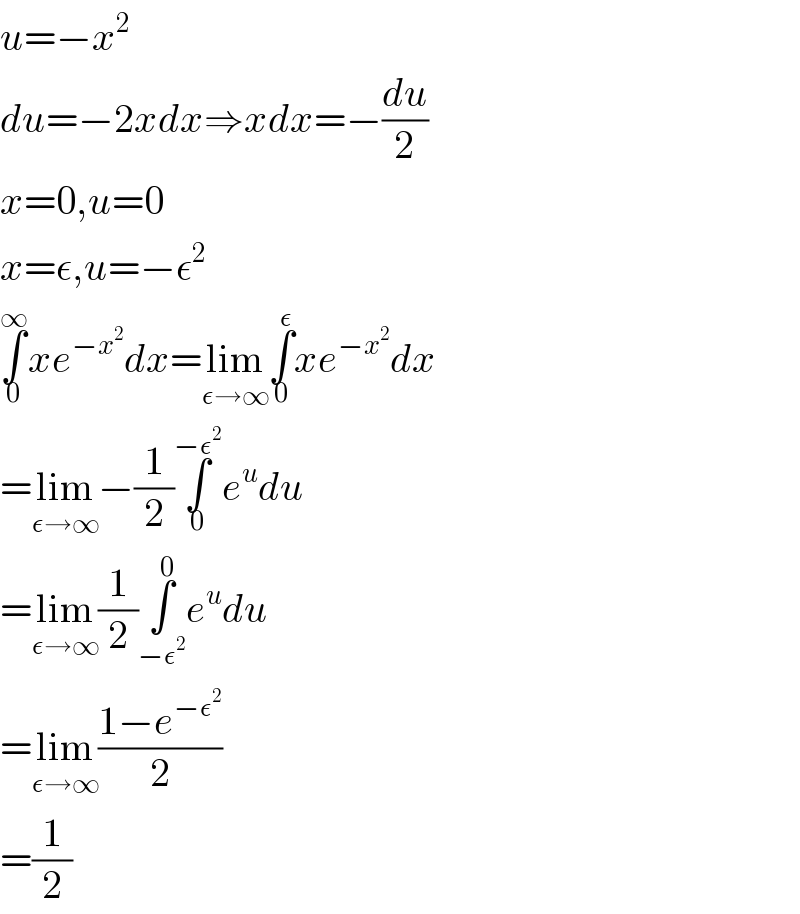
$${u}=−{x}^{\mathrm{2}} \\ $$$${du}=−\mathrm{2}{xdx}\Rightarrow{xdx}=−\frac{{du}}{\mathrm{2}} \\ $$$${x}=\mathrm{0},{u}=\mathrm{0} \\ $$$${x}=\epsilon,{u}=−\epsilon^{\mathrm{2}} \\ $$$$\underset{\mathrm{0}} {\overset{\infty} {\int}}{xe}^{−{x}^{\mathrm{2}} } {dx}=\underset{\epsilon\rightarrow\infty} {\mathrm{lim}}\underset{\mathrm{0}} {\overset{\epsilon} {\int}}{xe}^{−{x}^{\mathrm{2}} } {dx} \\ $$$$=\underset{\epsilon\rightarrow\infty} {\mathrm{lim}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{−\epsilon^{\mathrm{2}} } {\int}}{e}^{{u}} {du} \\ $$$$=\underset{\epsilon\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{2}}\underset{−\epsilon^{\mathrm{2}} } {\overset{\mathrm{0}} {\int}}{e}^{{u}} {du} \\ $$$$=\underset{\epsilon\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}−{e}^{−\epsilon^{\mathrm{2}} } }{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by swapnil last updated on 21/Oct/16

$$\mathrm{is}\:\epsilon>\mathrm{0}\:? \\ $$$$ \\ $$
