
Question Number 130306 by benjo_mathlover last updated on 24/Jan/21
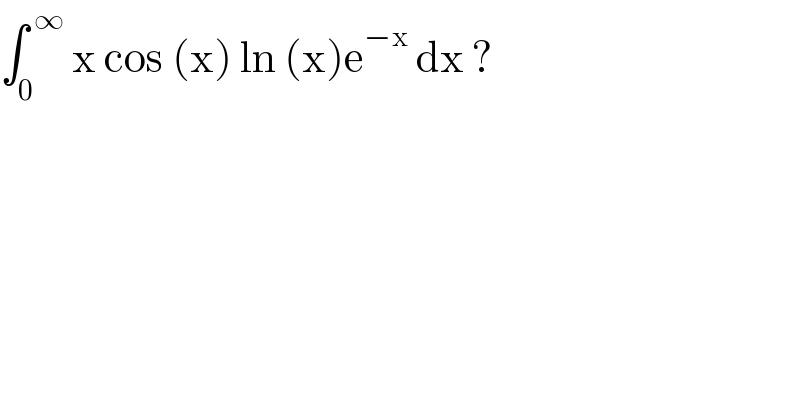
$$\int_{\mathrm{0}} ^{\:\infty} \:\mathrm{x}\:\mathrm{cos}\:\left(\mathrm{x}\right)\:\mathrm{ln}\:\left(\mathrm{x}\right)\mathrm{e}^{−\mathrm{x}} \:\mathrm{dx}\:?\: \\ $$
Answered by Dwaipayan Shikari last updated on 24/Jan/21
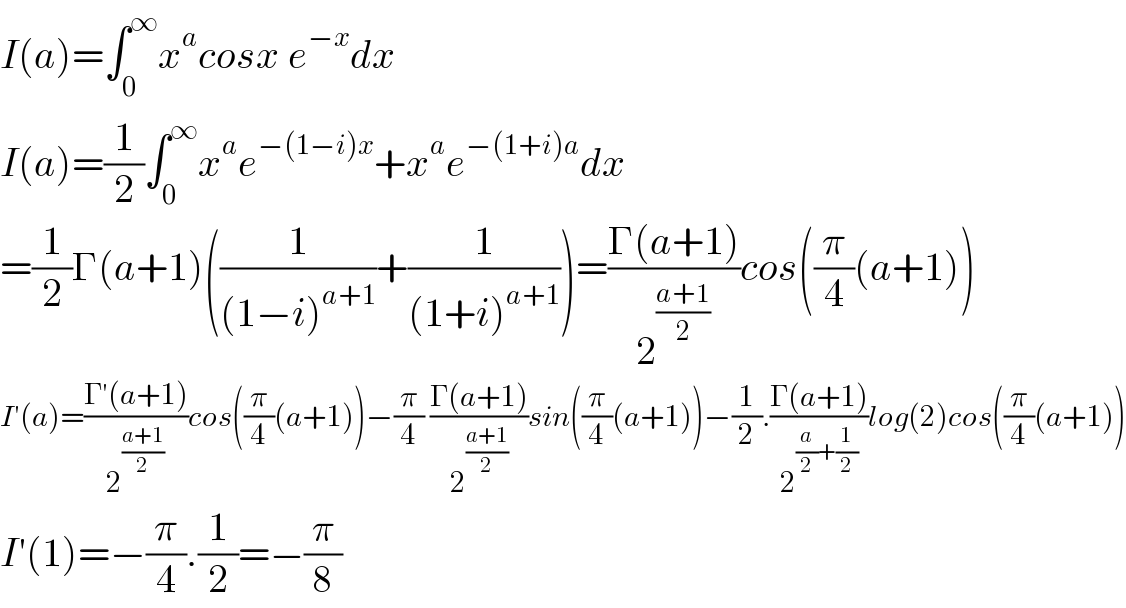
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} {x}^{{a}} {cosx}\:{e}^{−{x}} {dx} \\ $$$${I}\left({a}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} {x}^{{a}} {e}^{−\left(\mathrm{1}−{i}\right){x}} +{x}^{{a}} {e}^{−\left(\mathrm{1}+{i}\right){a}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left({a}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{\left(\mathrm{1}−{i}\right)^{{a}+\mathrm{1}} }+\frac{\mathrm{1}}{\left(\mathrm{1}+{i}\right)^{{a}+\mathrm{1}} }\right)=\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{cos}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right) \\ $$$${I}'\left({a}\right)=\frac{\Gamma'\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{cos}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right)−\frac{\pi}{\mathrm{4}}\:\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}+\mathrm{1}}{\mathrm{2}}} }{sin}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right)−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\Gamma\left({a}+\mathrm{1}\right)}{\mathrm{2}^{\frac{{a}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}} }{log}\left(\mathrm{2}\right){cos}\left(\frac{\pi}{\mathrm{4}}\left({a}+\mathrm{1}\right)\right) \\ $$$${I}'\left(\mathrm{1}\right)=−\frac{\pi}{\mathrm{4}}.\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\pi}{\mathrm{8}} \\ $$
Answered by mnjuly1970 last updated on 24/Jan/21
![Ω=Re∫_0 ^( ∞) xe^(−ix) ln(x)e^(−x) dx =Re∫_0 ^( ∞) xe^(−x(1+i)) ln(x)dx =Re((d/ds)∫_0 ^( ∞) x^s e^(−x(1+i)) dx)∣_(s=1) = Re((d/ds)[∫_0 ^( ∞) x^s e^(−x(1+i)) dx])∣_(s=1) Φ=∫_0 ^( ∞) x^(1+s) e^(−x(1+i)) dx=^(x(1+i)=t) ∫_0 ^( ∞) (t^s /((1+i)^(s+1) ))e^(−t) dt Φ=Γ(s+1)(1+i)^(−s−1) (dΦ/ds)=Γ′(s+1)(1+i)^(−s−1) ∣_(s=1) +[e^(−(s+1)ln(1+i)) ]^( ′) Γ(s+1)∣_(s=1) (dΦ/ds) ∣_(s=1) =Γ′(2)(1+i)^(−2) +(−ln(1+i))e^(−2ln(1+i)) Γ(2) =ψ(2)(2i)^(−1) +(−ln(1+i))e^(−ln(2i)) .1 =[−ψ(2)∗(i/2) =Imaginary]−ln((√2) e^((iπ)/4) )∗(1/(2i)) ∴ Ω =−(π/8) ...✓ ✓](Q130316.png)
$$\Omega=\mathscr{R}{e}\int_{\mathrm{0}} ^{\:\:\infty} {xe}^{−{ix}} {ln}\left({x}\right){e}^{−{x}} {dx} \\ $$$$\:\:\:\:\:=\mathscr{R}{e}\int_{\mathrm{0}} ^{\:\infty} {xe}^{−{x}\left(\mathrm{1}+{i}\right)} {ln}\left({x}\right){dx} \\ $$$$\:\:\:\:\:=\mathscr{R}{e}\left(\frac{{d}}{{ds}}\int_{\mathrm{0}} ^{\:\infty} {x}^{{s}} {e}^{−{x}\left(\mathrm{1}+{i}\right)} {dx}\right)\mid_{{s}=\mathrm{1}} \\ $$$$\:\:\:=\:\:\mathscr{R}{e}\left(\frac{{d}}{{ds}}\left[\int_{\mathrm{0}} ^{\:\infty} {x}^{{s}} {e}^{−{x}\left(\mathrm{1}+{i}\right)} {dx}\right]\right)\mid_{{s}=\mathrm{1}} \\ $$$$\:\:\:\Phi=\int_{\mathrm{0}} ^{\:\infty} {x}^{\mathrm{1}+{s}} {e}^{−{x}\left(\mathrm{1}+{i}\right)} {dx}\overset{{x}\left(\mathrm{1}+{i}\right)={t}} {=}\int_{\mathrm{0}} ^{\:\infty} \frac{{t}^{{s}} }{\left(\mathrm{1}+{i}\right)^{{s}+\mathrm{1}} }{e}^{−{t}} {dt} \\ $$$$\:\:\:\:\:\:\:\Phi=\Gamma\left({s}+\mathrm{1}\right)\left(\mathrm{1}+{i}\right)^{−{s}−\mathrm{1}} \\ $$$$\:\:\:\:\frac{{d}\Phi}{{ds}}=\Gamma'\left({s}+\mathrm{1}\right)\left(\mathrm{1}+{i}\right)^{−{s}−\mathrm{1}} \mid_{{s}=\mathrm{1}} +\left[{e}^{−\left({s}+\mathrm{1}\right){ln}\left(\mathrm{1}+{i}\right)} \overset{\:\:'} {\right]}\Gamma\left({s}+\mathrm{1}\right)\mid_{{s}=\mathrm{1}} \\ $$$$\:\:\:\frac{{d}\Phi}{{ds}}\:\mid_{{s}=\mathrm{1}} =\Gamma'\left(\mathrm{2}\right)\left(\mathrm{1}+{i}\right)^{−\mathrm{2}} +\left(−{ln}\left(\mathrm{1}+{i}\right)\right){e}^{−\mathrm{2}{ln}\left(\mathrm{1}+{i}\right)} \Gamma\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\psi\left(\mathrm{2}\right)\left(\mathrm{2}{i}\right)^{−\mathrm{1}} +\left(−{ln}\left(\mathrm{1}+{i}\right)\right){e}^{−{ln}\left(\mathrm{2}{i}\right)} .\mathrm{1} \\ $$$$=\left[−\psi\left(\mathrm{2}\right)\ast\frac{{i}}{\mathrm{2}}\:={Imaginary}\right]−{ln}\left(\sqrt{\mathrm{2}}\:{e}^{\frac{{i}\pi}{\mathrm{4}}} \right)\ast\frac{\mathrm{1}}{\mathrm{2}{i}} \\ $$$$\:\:\therefore\:\Omega\:=−\frac{\pi}{\mathrm{8}}\:...\checkmark\:\checkmark \\ $$$$\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\: \\ $$$$\:\: \\ $$
Commented by benjo_mathlover last updated on 24/Jan/21

$$\mathrm{the}\:\mathrm{ans}\:\mathrm{is}\:−\frac{\pi}{\mathrm{8}} \\ $$
Commented by mnjuly1970 last updated on 24/Jan/21

$${thanks}\:{alot}... \\ $$$$\: \\ $$
