
Question Number 130486 by benjo_mathlover last updated on 26/Jan/21
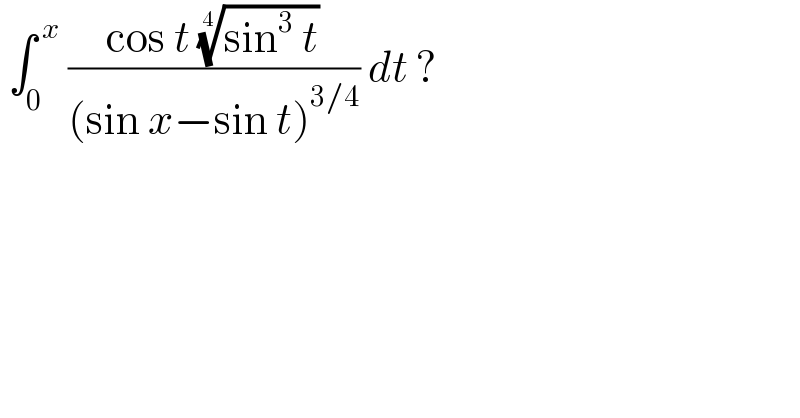
$$\:\int_{\mathrm{0}} ^{\:{x}} \:\frac{\mathrm{cos}\:{t}\:\sqrt[{\mathrm{4}}]{\mathrm{sin}^{\mathrm{3}} \:{t}}}{\left(\mathrm{sin}\:{x}−\mathrm{sin}\:{t}\right)^{\mathrm{3}/\mathrm{4}} }\:{dt}\:? \\ $$
Answered by MJS_new last updated on 26/Jan/21
![∫cos t (((sin t)/(sin x −sin t)))^(3/4) dt= [u=(((sin t)/(sin x −sin t)))^(1/4) → dt=((4((sin x −sin t)^5 sin^3 t)^(1/4) )/(sin x cos t))du] =4sin x ∫(u^6 /((u^4 +1)^2 ))du= [Ostrogradski] =sin x (−(u^3 /(u^4 +1))+3∫(u/(u^4 +1))du)= [3∫(u/(u^4 +1))du=((3(√2))/4)∫((u/(u^2 −(√2)u+1))−(u/(u^2 +(√2)u+1)))du] =sin x (−(u^3 /(u^4 +1))+((3(√2))/8)(ln ((u^2 −(√2)u+1)/(u^2 +(√2)u+1)) +2(arctan ((√2)u−1) +arctan ((√2)u+1)))) ... t=0 ⇒ u=0 t=x ⇒ u=+∞ (?) ⇒ answer is ((3π(√2))/4)sin x (?)](Q130495.png)
$$\int\mathrm{cos}\:{t}\:\left(\frac{\mathrm{sin}\:{t}}{\mathrm{sin}\:{x}\:−\mathrm{sin}\:{t}}\right)^{\mathrm{3}/\mathrm{4}} {dt}= \\ $$$$\:\:\:\:\:\left[{u}=\left(\frac{\mathrm{sin}\:{t}}{\mathrm{sin}\:{x}\:−\mathrm{sin}\:{t}}\right)^{\mathrm{1}/\mathrm{4}} \:\rightarrow\:{dt}=\frac{\mathrm{4}\left(\left(\mathrm{sin}\:{x}\:−\mathrm{sin}\:{t}\right)^{\mathrm{5}} \mathrm{sin}^{\mathrm{3}} \:{t}\right)^{\mathrm{1}/\mathrm{4}} }{\mathrm{sin}\:{x}\:\mathrm{cos}\:{t}}{du}\right] \\ $$$$=\mathrm{4sin}\:{x}\:\int\frac{{u}^{\mathrm{6}} }{\left({u}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} }{du}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}\right] \\ $$$$=\mathrm{sin}\:{x}\:\left(−\frac{{u}^{\mathrm{3}} }{{u}^{\mathrm{4}} +\mathrm{1}}+\mathrm{3}\int\frac{{u}}{{u}^{\mathrm{4}} +\mathrm{1}}{du}\right)= \\ $$$$\:\:\:\:\:\left[\mathrm{3}\int\frac{{u}}{{u}^{\mathrm{4}} +\mathrm{1}}{du}=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{4}}\int\left(\frac{{u}}{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}}−\frac{{u}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}}\right){du}\right] \\ $$$$=\mathrm{sin}\:{x}\:\left(−\frac{{u}^{\mathrm{3}} }{{u}^{\mathrm{4}} +\mathrm{1}}+\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{8}}\left(\mathrm{ln}\:\frac{{u}^{\mathrm{2}} −\sqrt{\mathrm{2}}{u}+\mathrm{1}}{{u}^{\mathrm{2}} +\sqrt{\mathrm{2}}{u}+\mathrm{1}}\:+\mathrm{2}\left(\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{u}−\mathrm{1}\right)\:+\mathrm{arctan}\:\left(\sqrt{\mathrm{2}}{u}+\mathrm{1}\right)\right)\right)\right) \\ $$$$... \\ $$$${t}=\mathrm{0}\:\Rightarrow\:{u}=\mathrm{0} \\ $$$${t}={x}\:\Rightarrow\:{u}=+\infty\:\left(?\right) \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{3}\pi\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{sin}\:{x}\:\left(?\right) \\ $$
Commented by benjo_mathlover last updated on 26/Jan/21

$${amazing} \\ $$
