Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 175343 by rexford last updated on 27/Aug/22

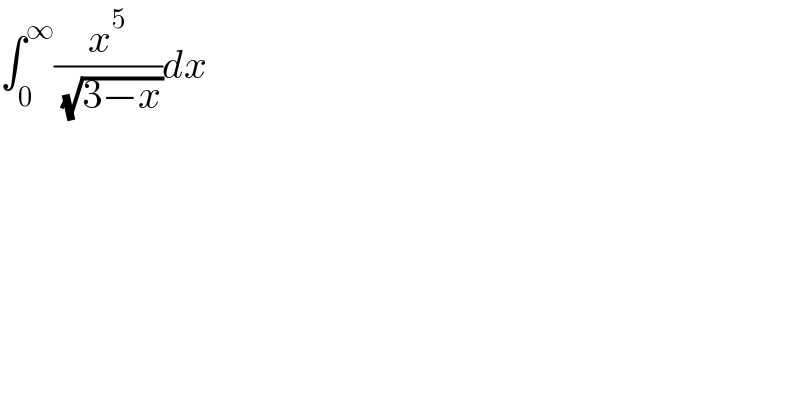
∫_0 ^∞ (x^5 /( (√(3−x))))dx

$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{5}} }{\:\sqrt{\mathrm{3}−{x}}}{dx} \\ $$

Commented by BaliramKumar last updated on 28/Aug/22

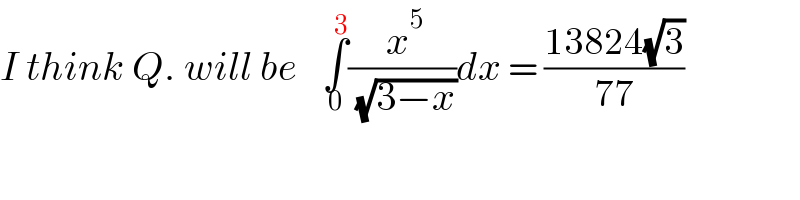
I think Q. will be ∫_0 ^3 (( x^5 )/( (√(3−x))))dx = ((13824(√3))/(77))

$${I}\:{think}\:{Q}.\:{will}\:{be}\:\:\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\:{x}^{\mathrm{5}} }{\:\sqrt{\mathrm{3}−{x}}}{dx}\:=\:\frac{\mathrm{13824}\sqrt{\mathrm{3}}}{\mathrm{77}} \\ $$

Answered by Ar Brandon last updated on 27/Aug/22

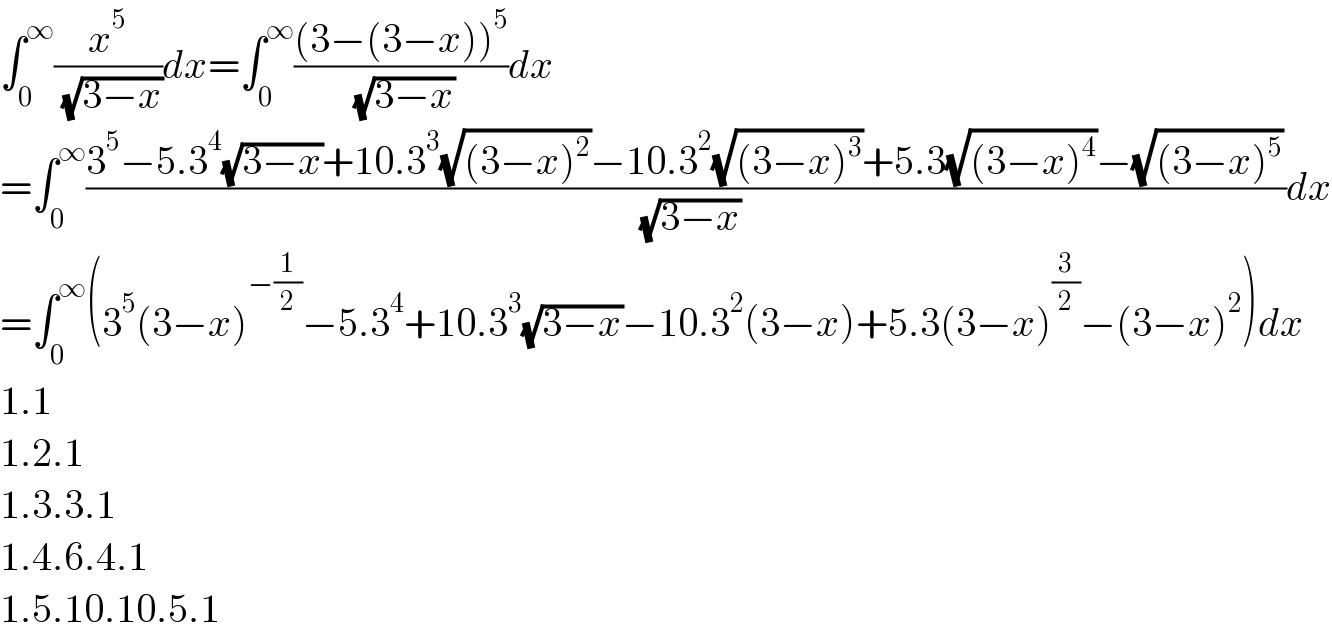
∫_0 ^∞ (x^5 /( (√(3−x))))dx=∫_0 ^∞ (((3−(3−x))^5 )/( (√(3−x))))dx =∫_0 ^∞ ((3^5 −5.3^4 (√(3−x))+10.3^3 (√((3−x)^2 ))−10.3^2 (√((3−x)^3 ))+5.3(√((3−x)^4 ))−(√((3−x)^5 )))/( (√(3−x))))dx =∫_0 ^∞ (3^5 (3−x)^(−(1/2)) −5.3^4 +10.3^3 (√(3−x))−10.3^2 (3−x)+5.3(3−x)^(3/2) −(3−x)^2 )dx 1.1 1.2.1 1.3.3.1 1.4.6.4.1 1.5.10.10.5.1

$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{5}} }{\:\sqrt{\mathrm{3}−{x}}}{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\left(\mathrm{3}−\left(\mathrm{3}−{x}\right)\right)^{\mathrm{5}} }{\:\sqrt{\mathrm{3}−{x}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{3}^{\mathrm{5}} −\mathrm{5}.\mathrm{3}^{\mathrm{4}} \sqrt{\mathrm{3}−{x}}+\mathrm{10}.\mathrm{3}^{\mathrm{3}} \sqrt{\left(\mathrm{3}−{x}\right)^{\mathrm{2}} }−\mathrm{10}.\mathrm{3}^{\mathrm{2}} \sqrt{\left(\mathrm{3}−{x}\right)^{\mathrm{3}} }+\mathrm{5}.\mathrm{3}\sqrt{\left(\mathrm{3}−{x}\right)^{\mathrm{4}} }−\sqrt{\left(\mathrm{3}−{x}\right)^{\mathrm{5}} }}{\:\sqrt{\mathrm{3}−{x}}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\mathrm{3}^{\mathrm{5}} \left(\mathrm{3}−{x}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} −\mathrm{5}.\mathrm{3}^{\mathrm{4}} +\mathrm{10}.\mathrm{3}^{\mathrm{3}} \sqrt{\mathrm{3}−{x}}−\mathrm{10}.\mathrm{3}^{\mathrm{2}} \left(\mathrm{3}−{x}\right)+\mathrm{5}.\mathrm{3}\left(\mathrm{3}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} −\left(\mathrm{3}−{x}\right)^{\mathrm{2}} \right){dx} \\ $$$$\mathrm{1}.\mathrm{1} \\ $$$$\mathrm{1}.\mathrm{2}.\mathrm{1} \\ $$$$\mathrm{1}.\mathrm{3}.\mathrm{3}.\mathrm{1} \\ $$$$\mathrm{1}.\mathrm{4}.\mathrm{6}.\mathrm{4}.\mathrm{1} \\ $$$$\mathrm{1}.\mathrm{5}.\mathrm{10}.\mathrm{10}.\mathrm{5}.\mathrm{1} \\ $$

Commented by Ar Brandon last updated on 27/Aug/22

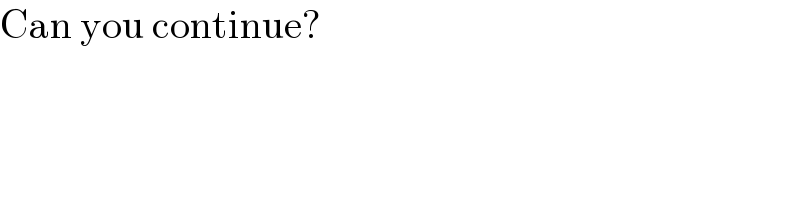
Can you continue?

$$\mathrm{Can}\:\mathrm{you}\:\mathrm{continue}? \\ $$

Answered by CElcedricjunior last updated on 27/Aug/22

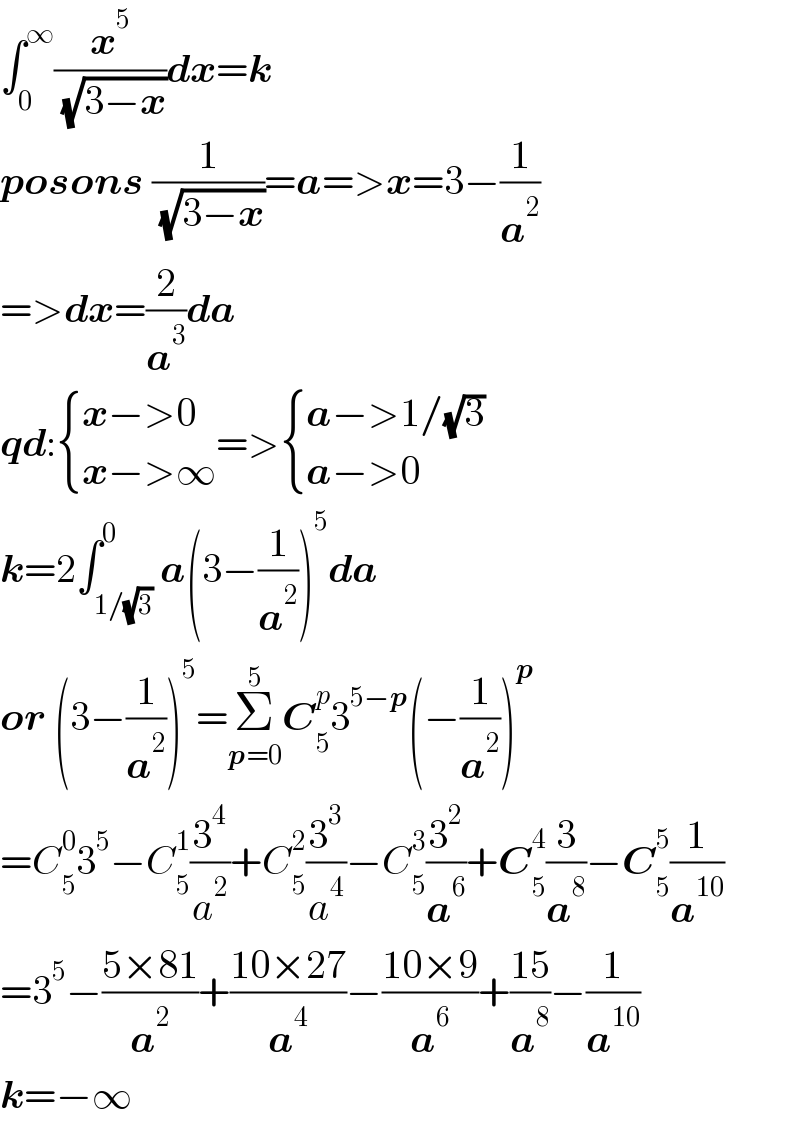
∫_0 ^∞ (x^5 /( (√(3−x))))dx=k posons (1/( (√(3−x))))=a=>x=3−(1/a^2 ) =>dx=(2/a^3 )da qd: { ((x−>0)),((x−>∞)) :}=> { ((a−>1/(√3))),((a−>0)) :} k=2∫_(1/(√3)) ^0 a(3−(1/a^2 ))^5 da or (3−(1/a^2 ))^5 =Σ_(p=0) ^5 C_5 ^p 3^(5−p) (−(1/a^2 ))^p =C_5 ^0 3^5 −C_5 ^1 (3^4 /a^2 )+C_5 ^2 (3^3 /a^4 )−C_5 ^3 (3^2 /a^6 )+C_5 ^4 (3/a^8 )−C_5 ^5 (1/a^(10) ) =3^5 −((5×81)/a^2 )+((10×27)/a^4 )−((10×9)/a^6 )+((15)/a^8 )−(1/a^(10) ) k=−∞

$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{{x}}^{\mathrm{5}} }{\:\sqrt{\mathrm{3}−\boldsymbol{{x}}}}\boldsymbol{{dx}}=\boldsymbol{{k}} \\ $$$$\boldsymbol{{posons}}\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}−\boldsymbol{{x}}}}=\boldsymbol{{a}}=>\boldsymbol{{x}}=\mathrm{3}−\frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{2}} } \\ $$$$=>\boldsymbol{{dx}}=\frac{\mathrm{2}}{\boldsymbol{{a}}^{\mathrm{3}} }\boldsymbol{{da}} \\ $$$$\boldsymbol{{qd}}:\begin{cases}{\boldsymbol{{x}}−>\mathrm{0}}\\{\boldsymbol{{x}}−>\infty}\end{cases}=>\begin{cases}{\boldsymbol{{a}}−>\mathrm{1}/\sqrt{\mathrm{3}}}\\{\boldsymbol{{a}}−>\mathrm{0}}\end{cases} \\ $$$$\boldsymbol{{k}}=\mathrm{2}\int_{\mathrm{1}/\sqrt{\mathrm{3}}} ^{\mathrm{0}} \boldsymbol{{a}}\left(\mathrm{3}−\frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{2}} }\right)^{\mathrm{5}} \boldsymbol{{da}} \\ $$$$\boldsymbol{{or}}\:\left(\mathrm{3}−\frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{2}} }\right)^{\mathrm{5}} =\underset{\boldsymbol{{p}}=\mathrm{0}} {\overset{\mathrm{5}} {\sum}}\boldsymbol{{C}}_{\mathrm{5}} ^{{p}} \mathrm{3}^{\mathrm{5}−\boldsymbol{{p}}} \left(−\frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{2}} }\right)^{\boldsymbol{{p}}} \\ $$$$={C}_{\mathrm{5}} ^{\mathrm{0}} \mathrm{3}^{\mathrm{5}} −{C}_{\mathrm{5}} ^{\mathrm{1}} \frac{\mathrm{3}^{\mathrm{4}} }{{a}^{\mathrm{2}} }+{C}_{\mathrm{5}} ^{\mathrm{2}} \frac{\mathrm{3}^{\mathrm{3}} }{{a}^{\mathrm{4}} }−{C}_{\mathrm{5}} ^{\mathrm{3}} \frac{\mathrm{3}^{\mathrm{2}} }{\boldsymbol{{a}}^{\mathrm{6}} }+\boldsymbol{{C}}_{\mathrm{5}} ^{\mathrm{4}} \frac{\mathrm{3}}{\boldsymbol{{a}}^{\mathrm{8}} }−\boldsymbol{{C}}_{\mathrm{5}} ^{\mathrm{5}} \frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{10}} } \\ $$$$=\mathrm{3}^{\mathrm{5}} −\frac{\mathrm{5}×\mathrm{81}}{\boldsymbol{{a}}^{\mathrm{2}} }+\frac{\mathrm{10}×\mathrm{27}}{\boldsymbol{{a}}^{\mathrm{4}} }−\frac{\mathrm{10}×\mathrm{9}}{\boldsymbol{{a}}^{\mathrm{6}} }+\frac{\mathrm{15}}{\boldsymbol{{a}}^{\mathrm{8}} }−\frac{\mathrm{1}}{\boldsymbol{{a}}^{\mathrm{10}} } \\ $$$$\boldsymbol{{k}}=−\infty \\ $$

Answered by MJS_new last updated on 28/Aug/22

∫(x^5 /( (√(3−x))))dx= [t=3−x → dx=−dt] =∫(((3−t)^5 )/( (√t)))dt= =∫(t^(9/2) −15t^(7/2) +90t^(5/2) −270t^(3/2) +405t^(1/2) −243t^(−1/2) )dt= =(2/(11))t^(11/2) −((10)/3)t^(9/2) +((180)/7)t^(7/2) −108t^(5/2) +270t^(3/2) −486t^(1/2) = ...=F(x)+C F(x)=−((2(√(3−x))(21x^5 +70x^4 +240x^3 +864x^2 +3456x+20736))/(231)) F(0)=−((13824(√3))/(77)) lim_(x→∞) F(x) is not defined ⇒ integral doesn′t exist

$$\int\frac{{x}^{\mathrm{5}} }{\:\sqrt{\mathrm{3}−{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{3}−{x}\:\rightarrow\:{dx}=−{dt}\right] \\ $$$$=\int\frac{\left(\mathrm{3}−{t}\right)^{\mathrm{5}} }{\:\sqrt{{t}}}{dt}= \\ $$$$=\int\left({t}^{\mathrm{9}/\mathrm{2}} −\mathrm{15}{t}^{\mathrm{7}/\mathrm{2}} +\mathrm{90}{t}^{\mathrm{5}/\mathrm{2}} −\mathrm{270}{t}^{\mathrm{3}/\mathrm{2}} +\mathrm{405}{t}^{\mathrm{1}/\mathrm{2}} −\mathrm{243}{t}^{−\mathrm{1}/\mathrm{2}} \right){dt}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{11}}{t}^{\mathrm{11}/\mathrm{2}} −\frac{\mathrm{10}}{\mathrm{3}}{t}^{\mathrm{9}/\mathrm{2}} +\frac{\mathrm{180}}{\mathrm{7}}{t}^{\mathrm{7}/\mathrm{2}} −\mathrm{108}{t}^{\mathrm{5}/\mathrm{2}} +\mathrm{270}{t}^{\mathrm{3}/\mathrm{2}} −\mathrm{486}{t}^{\mathrm{1}/\mathrm{2}} = \\ $$$$...={F}\left({x}\right)+{C} \\ $$$${F}\left({x}\right)=−\frac{\mathrm{2}\sqrt{\mathrm{3}−{x}}\left(\mathrm{21}{x}^{\mathrm{5}} +\mathrm{70}{x}^{\mathrm{4}} +\mathrm{240}{x}^{\mathrm{3}} +\mathrm{864}{x}^{\mathrm{2}} +\mathrm{3456}{x}+\mathrm{20736}\right)}{\mathrm{231}} \\ $$$${F}\left(\mathrm{0}\right)=−\frac{\mathrm{13824}\sqrt{\mathrm{3}}}{\mathrm{77}} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:{F}\left({x}\right)\:\:\mathrm{is}\:\mathrm{not}\:\mathrm{defined} \\ $$$$\Rightarrow\:\mathrm{integral}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com