
Question Number 65203 by arcana last updated on 26/Jul/19
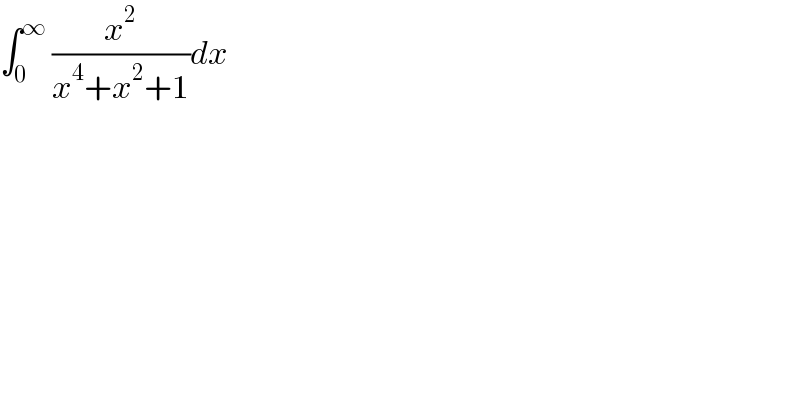
$$\int_{\mathrm{0}} ^{\infty} \:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$
Commented by mathmax by abdo last updated on 26/Jul/19

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:\Rightarrow\mathrm{2}{I}\:=\int_{−\infty} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{4}} \:+{x}^{\mathrm{2}} +\mathrm{1}}{dx}\:{let} \\ $$$$\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{{z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}}\:\:\:{poles}\:{of}\:\varphi? \\ $$$${z}^{\mathrm{4}} \:+{z}^{\mathrm{2}} \:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} +{t}\:+\mathrm{1}\:=\mathrm{0}\:\:\left({t}={z}^{\mathrm{2}} \right) \\ $$$$\Delta\:=\mathrm{1}−\mathrm{4}\:=−\mathrm{3}\:=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${t}_{\mathrm{1}} ={e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \:\:\:{and}\:\:{t}_{\mathrm{2}} ={e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \:\:\Rightarrow{t}^{\mathrm{2}} \:+{t}+\mathrm{1}\:=\left({t}−{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left({t}−{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right) \\ $$$$=\left({z}^{\mathrm{2}} −{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left({z}^{\mathrm{2}} −{e}^{−\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\:\Rightarrow\varphi\left({z}\right)\:=\frac{{z}^{\mathrm{2}} }{\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:\overset{−} {+}{e}^{\frac{{i}\pi}{\mathrm{3}}} \:{and}\:\overset{−} {+}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\:{residus}\:{theorem}\:{give} \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:+{Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\right\} \\ $$$$\:{Res}\left(\varphi,{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\:={lim}_{{z}\rightarrow{e}^{\frac{{i}\pi}{\mathrm{3}}} } \:\:\:\:\left({z}−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\varphi\left({z}\right)=\frac{{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} }{\mathrm{2}{e}^{\frac{{i}\pi}{\mathrm{3}}} \left({e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} −{e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}\left(\mathrm{2}{isin}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\right)}\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{4}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}\:=\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}} \\ $$$${Res}\left(\varphi,−{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:={lim}_{{z}\rightarrow{e}^{−\frac{{i}\pi}{\mathrm{3}}} } \:\:\:\left({z}+{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)\:=\:\frac{{e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} }{\left({e}^{−\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} −{e}^{\frac{{i}\mathrm{2}\pi}{\mathrm{3}}} \right)\left(−\mathrm{2}{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right)} \\ $$$$=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{−\mathrm{2}{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\left(−\mathrm{2}\right)}\:=\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:\Rightarrow\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi\left\{\frac{{e}^{\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\:+\frac{{e}^{−\frac{{i}\pi}{\mathrm{3}}} }{\mathrm{2}{i}\sqrt{\mathrm{3}}}\right\} \\ $$$$=\frac{\pi}{\sqrt{\mathrm{3}}}\left\{\mathrm{2}{cos}\left(\frac{\pi}{\mathrm{3}}\right)\:=\frac{\pi}{\sqrt{\mathrm{3}}}\:\left(\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\frac{\pi}{\sqrt{\mathrm{3}}}\:\Rightarrow\:{I}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}}\:.\right. \\ $$
Answered by Tanmay chaudhury last updated on 26/Jul/19

$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\mathrm{1}}{dx} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{d}\left({x}−\frac{\mathrm{1}}{{x}}\right)}{\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{d}\left({x}+\frac{\mathrm{1}}{{x}}\right)}{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{x}−\frac{\mathrm{1}}{{x}}}{\sqrt{\mathrm{3}}}\right)+\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}×\mathrm{1}}{ln}\left(\frac{{x}+\frac{\mathrm{1}}{{x}}−\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}+\mathrm{1}}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(\infty\right)−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}{tan}^{−\mathrm{1}} \left(−\infty\right)+\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{{x}}}{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{{x}}}\right)_{{x}=\infty} −\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\frac{{x}^{\mathrm{2}} +\mathrm{1}−{x}}{{x}^{\mathrm{2}} +\mathrm{1}+{x}}\right)_{{x}=\mathrm{0}} \\ $$$$\left.=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}×\frac{\pi}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{4}}×{ln}\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mathrm{1} \\ $$$$=\frac{\pi}{\mathrm{2}\sqrt{\mathrm{3}}} \\ $$
Commented by arcana last updated on 26/Jul/19
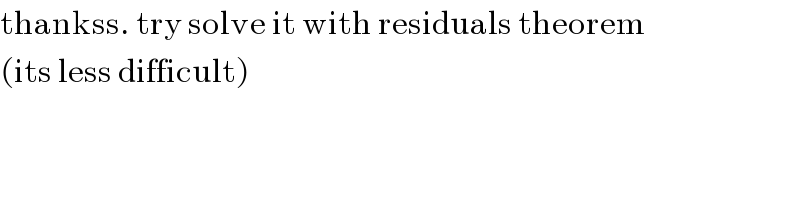
$$\mathrm{thankss}.\:\mathrm{try}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{with}\:\mathrm{residuals}\:\mathrm{theorem} \\ $$$$\left(\mathrm{its}\:\mathrm{less}\:\mathrm{difficult}\right) \\ $$
Commented by Tanmay chaudhury last updated on 26/Jul/19

$${ok}\:{sir}... \\ $$
