Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 218748 by MrGaster last updated on 15/Apr/25

∫_0 ^∞ ((x^2 cos x)/(cosh 2x−cos x))−((2x^2 )/(e^(4x) −2e^(2x) cos x+1))dx,lemma:Σ_(k=1) ^(+∞) ((cos kx)/p^k )=((p cos x−1)/(p^2 −2p cos x+1)),p>1

$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} \mathrm{cos}\:{x}}{\mathrm{cosh}\:\mathrm{2}{x}−\mathrm{cos}\:{x}}−\frac{\mathrm{2}{x}^{\mathrm{2}} }{\mathrm{e}^{\mathrm{4}{x}} −\mathrm{2}{e}^{\mathrm{2}{x}} \mathrm{cos}\:{x}+\mathrm{1}}{dx},\mathrm{lemma}:\underset{{k}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\mathrm{cos}\:{kx}}{{p}^{{k}} }=\frac{\mathrm{p}\:\mathrm{cos}\:{x}−\mathrm{1}}{{p}^{\mathrm{2}} −\mathrm{2}{p}\:\mathrm{cos}\:{x}+\mathrm{1}},{p}>\mathrm{1} \\ $$

Answered by MrGaster last updated on 17/Apr/25

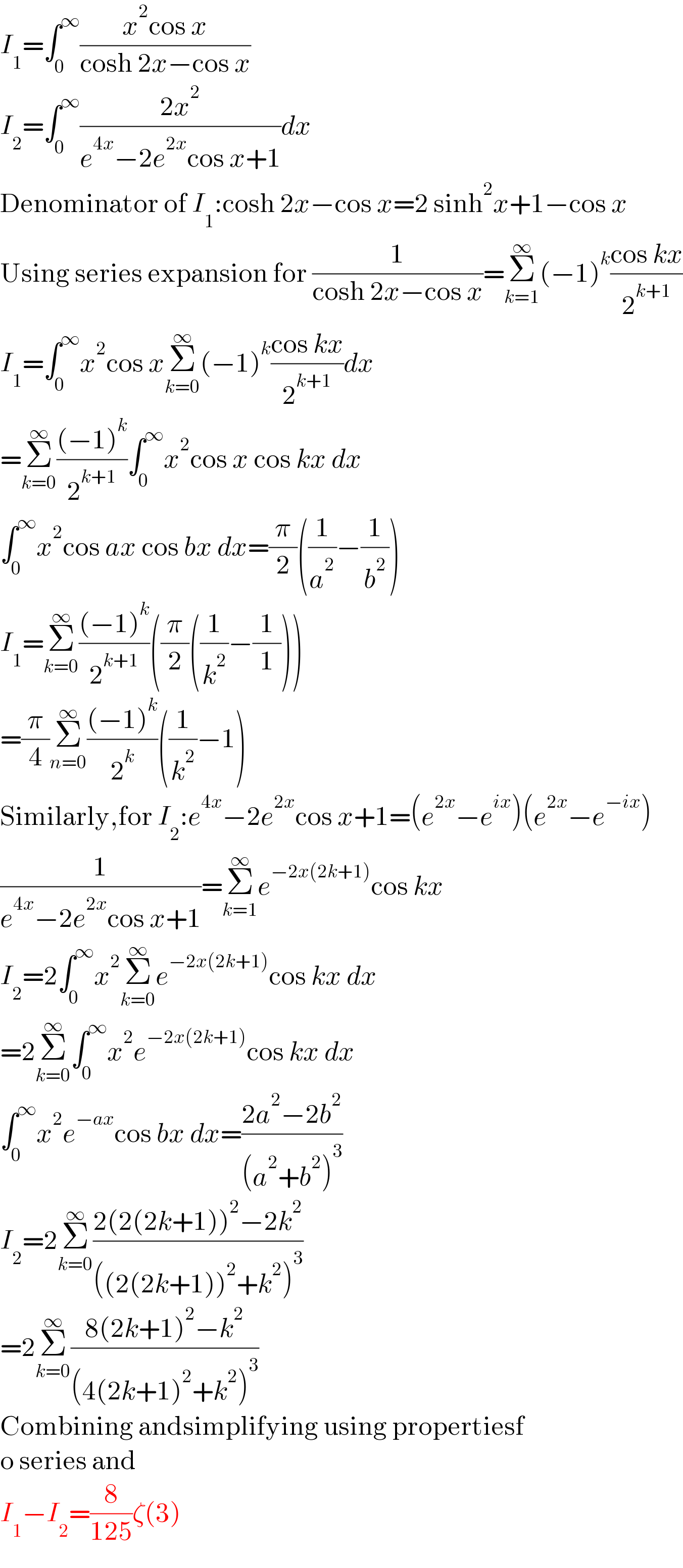
I_1 =∫_0 ^∞ ((x^2 cos x)/(cosh 2x−cos x)) I_2 =∫_0 ^∞ ((2x^2 )/(e^(4x) −2e^(2x) cos x+1))dx Denominator of I_1 :cosh 2x−cos x=2 sinh^2 x+1−cos x Using series expansion for (1/(cosh 2x−cos x))=Σ_(k=1) ^∞ (−1)^k ((cos kx)/2^(k+1) ) I_1 =∫_0 ^∞ x^2 cos xΣ_(k=0) ^∞ (−1)^k ((cos kx)/2^(k+1) )dx =Σ_(k=0) ^∞ (((−1)^k )/2^(k+1) )∫_0 ^∞ x^2 cos x cos kx dx ∫_0 ^∞ x^2 cos ax cos bx dx=(π/2)((1/a^2 )−(1/b^2 )) I_1 =Σ_(k=0) ^∞ (((−1)^k )/2^(k+1) )((π/2)((1/k^2 )−(1/1))) =(π/4)Σ_(n=0) ^∞ (((−1)^k )/2^k )((1/k^2 )−1) Similarly,for I_2 :e^(4x) −2e^(2x) cos x+1=(e^(2x) −e^(ix) )(e^(2x) −e^(−ix) ) (1/(e^(4x) −2e^(2x) cos x+1))=Σ_(k=1) ^∞ e^(−2x(2k+1)) cos kx I_2 =2∫_0 ^∞ x^2 Σ_(k=0) ^∞ e^(−2x(2k+1)) cos kx dx =2Σ_(k=0) ^∞ ∫_0 ^∞ x^2 e^(−2x(2k+1)) cos kx dx ∫_0 ^∞ x^2 e^(−ax) cos bx dx=((2a^2 −2b^2 )/((a^2 +b^2 )^3 )) I_2 =2Σ_(k=0) ^∞ ((2(2(2k+1))^2 −2k^2 )/(((2(2k+1))^2 +k^2 )^3 )) =2Σ_(k=0) ^∞ ((8(2k+1)^2 −k^2 )/((4(2k+1)^2 +k^2 )^3 )) Combining andsimplifying using propertiesf o series and I_1 −I_2 =(8/(125))ζ(3)

$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} \mathrm{cos}\:{x}}{\mathrm{cosh}\:\mathrm{2}{x}−\mathrm{cos}\:{x}} \\ $$$${I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{x}^{\mathrm{2}} }{{e}^{\mathrm{4}{x}} −\mathrm{2}{e}^{\mathrm{2}{x}} \mathrm{cos}\:{x}+\mathrm{1}}{dx} \\ $$$$\mathrm{Denominator}\:\mathrm{of}\:{I}_{\mathrm{1}} :\mathrm{cosh}\:\mathrm{2}{x}−\mathrm{cos}\:{x}=\mathrm{2}\:\mathrm{sinh}^{\mathrm{2}} {x}+\mathrm{1}−\mathrm{cos}\:{x} \\ $$$$\mathrm{Using}\:\mathrm{series}\:\mathrm{expansion}\:\mathrm{for}\:\frac{\mathrm{1}}{\mathrm{cosh}\:\mathrm{2}{x}−\mathrm{cos}\:{x}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \frac{\mathrm{cos}\:{kx}}{\mathrm{2}^{{k}+\mathrm{1}} } \\ $$$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} \mathrm{cos}\:{x}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{k}} \frac{\mathrm{cos}\:{kx}}{\mathrm{2}^{{k}+\mathrm{1}} }{dx} \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}+\mathrm{1}} }\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} \mathrm{cos}\:{x}\:\mathrm{cos}\:{kx}\:{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} \mathrm{cos}\:{ax}\:\mathrm{cos}\:{bx}\:{dx}=\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }−\frac{\mathrm{1}}{{b}^{\mathrm{2}} }\right) \\ $$$${I}_{\mathrm{1}} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}+\mathrm{1}} }\left(\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{1}}\right)\right) \\ $$$$=\frac{\pi}{\mathrm{4}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}} }{\mathrm{2}^{{k}} }\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{1}\right) \\ $$$$\mathrm{Similarly},\mathrm{for}\:{I}_{\mathrm{2}} :{e}^{\mathrm{4}{x}} −\mathrm{2}{e}^{\mathrm{2}{x}} \mathrm{cos}\:{x}+\mathrm{1}=\left({e}^{\mathrm{2}{x}} −{e}^{{ix}} \right)\left({e}^{\mathrm{2}{x}} −{e}^{−{ix}} \right) \\ $$$$\frac{\mathrm{1}}{{e}^{\mathrm{4}{x}} −\mathrm{2}{e}^{\mathrm{2}{x}} \mathrm{cos}\:{x}+\mathrm{1}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{e}^{−\mathrm{2}{x}\left(\mathrm{2}{k}+\mathrm{1}\right)} \mathrm{cos}\:{kx} \\ $$$${I}_{\mathrm{2}} =\mathrm{2}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{e}^{−\mathrm{2}{x}\left(\mathrm{2}{k}+\mathrm{1}\right)} \mathrm{cos}\:{kx}\:{dx} \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−\mathrm{2}{x}\left(\mathrm{2}{k}+\mathrm{1}\right)} \mathrm{cos}\:{kx}\:{dx} \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−{ax}} \mathrm{cos}\:{bx}\:{dx}=\frac{\mathrm{2}{a}^{\mathrm{2}} −\mathrm{2}{b}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)^{\mathrm{3}} }\: \\ $$$${I}_{\mathrm{2}} =\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}\left(\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\right)^{\mathrm{2}} −\mathrm{2}{k}^{\mathrm{2}} }{\left(\left(\mathrm{2}\left(\mathrm{2}{k}+\mathrm{1}\right)\right)^{\mathrm{2}} +{k}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$=\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{8}\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} −{k}^{\mathrm{2}} }{\left(\mathrm{4}\left(\mathrm{2}{k}+\mathrm{1}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} \right)^{\mathrm{3}} } \\ $$$$\mathrm{Combining}\:\mathrm{andsimplifying}\:\mathrm{using}\:\mathrm{propertiesf} \\ $$$$\mathrm{o}\:\mathrm{series}\:\mathrm{and}\: \\ $$$${I}_{\mathrm{1}} −{I}_{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{125}}\zeta\left(\mathrm{3}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com