Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 210354 by klipto last updated on 08/Aug/24

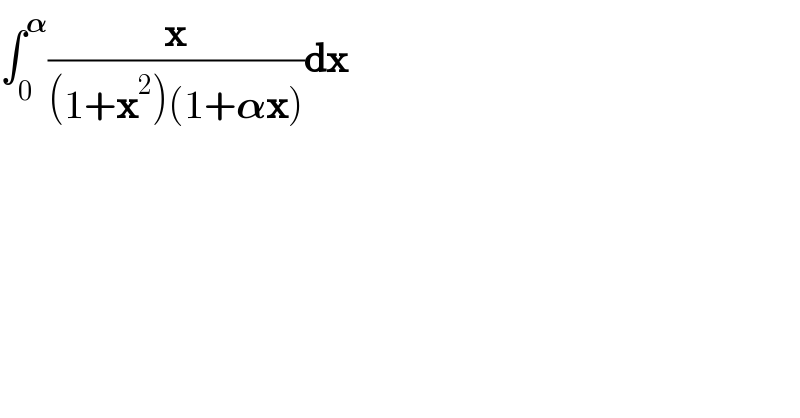
∫_0 ^𝛂 (x/((1+x^2 )(1+𝛂x)))dx

$$\int_{\mathrm{0}} ^{\boldsymbol{\alpha}} \frac{\boldsymbol{\mathrm{x}}}{\left(\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\left(\mathrm{1}+\boldsymbol{\alpha\mathrm{x}}\right)}\boldsymbol{\mathrm{dx}} \\ $$

Answered by klipto last updated on 08/Aug/24

$$ \\ $$

Answered by Frix last updated on 08/Aug/24

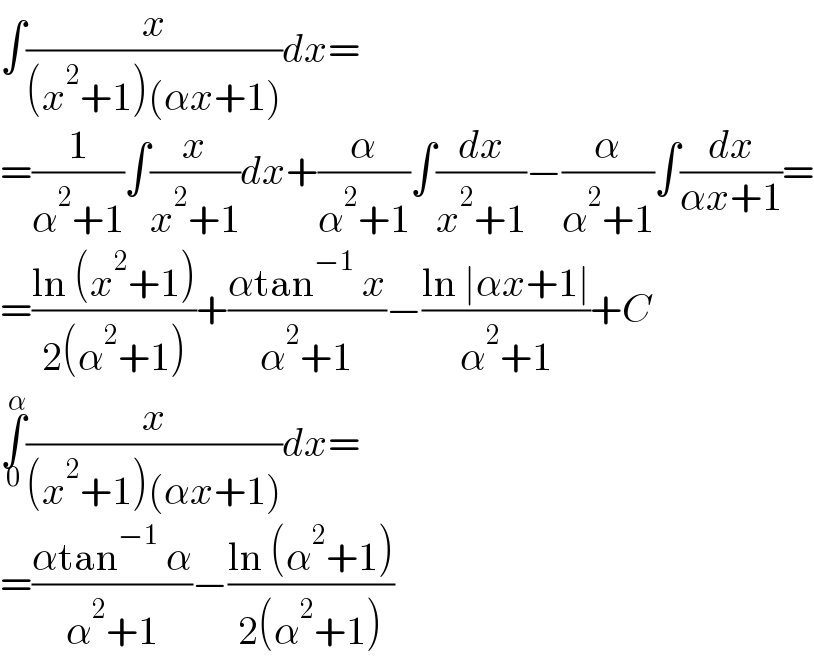
∫(x/((x^2 +1)(αx+1)))dx= =(1/(α^2 +1))∫(x/(x^2 +1))dx+(α/(α^2 +1))∫(dx/(x^2 +1))−(α/(α^2 +1))∫(dx/(αx+1))= =((ln (x^2 +1))/(2(α^2 +1)))+((αtan^(−1) x)/(α^2 +1))−((ln ∣αx+1∣)/(α^2 +1))+C ∫_0 ^α (x/((x^2 +1)(αx+1)))dx= =((αtan^(−1) α)/(α^2 +1))−((ln (α^2 +1))/(2(α^2 +1)))

$$\int\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\alpha{x}+\mathrm{1}\right)}{dx}= \\ $$$$=\frac{\mathrm{1}}{\alpha^{\mathrm{2}} +\mathrm{1}}\int\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}+\frac{\alpha}{\alpha^{\mathrm{2}} +\mathrm{1}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}−\frac{\alpha}{\alpha^{\mathrm{2}} +\mathrm{1}}\int\frac{{dx}}{\alpha{x}+\mathrm{1}}= \\ $$$$=\frac{\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}\left(\alpha^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\alpha\mathrm{tan}^{−\mathrm{1}} \:{x}}{\alpha^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{ln}\:\mid\alpha{x}+\mathrm{1}\mid}{\alpha^{\mathrm{2}} +\mathrm{1}}+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\alpha} {\int}}\frac{{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left(\alpha{x}+\mathrm{1}\right)}{dx}= \\ $$$$=\frac{\alpha\mathrm{tan}^{−\mathrm{1}} \:\alpha}{\alpha^{\mathrm{2}} +\mathrm{1}}−\frac{\mathrm{ln}\:\left(\alpha^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}\left(\alpha^{\mathrm{2}} +\mathrm{1}\right)} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com