
Question Number 156860 by amin96 last updated on 16/Oct/21
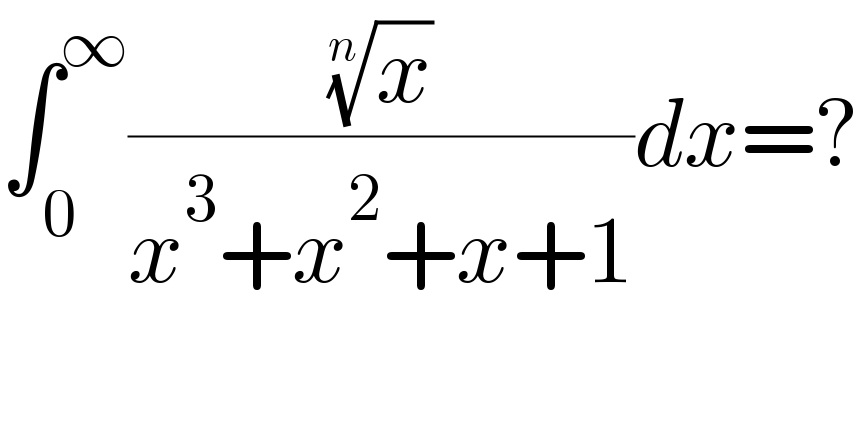
$$\int_{\mathrm{0}} ^{\infty} \frac{\sqrt[{{n}}]{{x}}}{{x}^{\mathrm{3}} +{x}^{\mathrm{2}} +{x}+\mathrm{1}}{dx}=? \\ $$
Answered by mindispower last updated on 16/Oct/21

$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{a}} {dx}}{\mathrm{1}+{x}+..+{x}^{{m}} },{a}\in\left[\mathrm{0},{m}−\mathrm{1}\left[,{m}\in\mathbb{N}−\left\{\mathrm{0},\mathrm{1}\right\}\right.\right. \\ $$$${f}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} }{\mathrm{1}+{x}..+{x}^{{m}} }{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{−{a}} {x}^{{m}−\mathrm{2}} }{\left(\mathrm{1}+{x}..+{x}^{{m}} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} \left(\mathrm{1}−{x}\right)}{\mathrm{1}−{x}^{{m}+\mathrm{1}} }+\frac{{x}^{{m}−\left({a}+\mathrm{2}\right)} \left(\mathrm{1}−{x}\right)}{\mathrm{1}−{x}^{{m}+\mathrm{1}} }{dx} \\ $$$${x}^{{m}+\mathrm{1}} ={t} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\frac{{a}}{{m}+\mathrm{1}}} \left(\mathrm{1}−{t}^{\frac{\mathrm{1}}{{m}+\mathrm{1}}} \right)}{\mathrm{1}−{t}}.{t}^{−\frac{{m}}{{m}+\mathrm{1}}} \frac{{dt}}{{m}+\mathrm{1}}+\frac{\mathrm{1}}{{m}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\frac{{m}−\left({a}+\mathrm{2}\right)}{{m}+\mathrm{1}}} \left(\mathrm{1}−{t}^{\frac{\mathrm{1}}{{m}+\mathrm{1}}} \right)}{\mathrm{1}−{t}}{t}^{−\frac{{m}}{{m}+\mathrm{1}}} {dt} \\ $$$$=\frac{\mathrm{1}}{{m}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\frac{{a}−{m}}{{m}+\mathrm{1}}} −{t}^{\frac{\mathrm{1}+{a}−{m}}{{m}+\mathrm{1}}} }{\mathrm{1}−{t}}{dt}+\frac{\mathrm{1}}{{m}+\mathrm{1}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{−\frac{{a}+\mathrm{2}}{{m}+\mathrm{1}}} −{t}^{\frac{\mathrm{1}−\left({a}+\mathrm{2}\right)}{{m}+\mathrm{1}}} }{\mathrm{1}−{t}}{dt} \\ $$$${recall} \\ $$$$\Psi\left(\mathrm{1}+{s}\right)=−\gamma+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}^{{s}} }{\mathrm{1}−{x}}{dx} \\ $$$${we}\:{get} \\ $$$$=\frac{\mathrm{1}}{{m}+\mathrm{1}}\left(\Psi\left(\frac{\mathrm{1}+{a}−{m}}{{m}+\mathrm{1}}+\mathrm{1}\right)−\Psi\left(\frac{{a}−{m}}{{m}+\mathrm{1}}+\mathrm{1}\right)+\Psi\left(\frac{\mathrm{1}−{a}−\mathrm{2}}{{m}+\mathrm{1}}+\mathrm{1}\right)−\Psi\left(\frac{−{a}−\mathrm{2}}{{m}+\mathrm{1}}+\mathrm{1}\right)\right) \\ $$$${put}\:{a}=\frac{\mathrm{1}}{{n}},{m}=\mathrm{3} \\ $$
Commented by mnjuly1970 last updated on 16/Oct/21
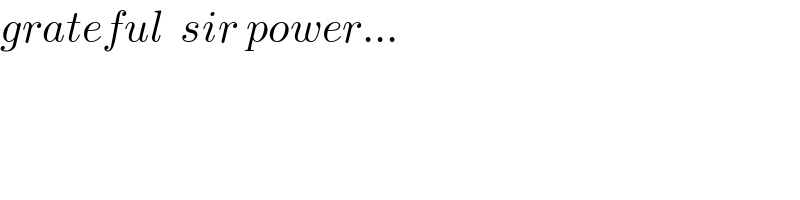
$${grateful}\:\:{sir}\:{power}... \\ $$
Commented by amin96 last updated on 16/Oct/21
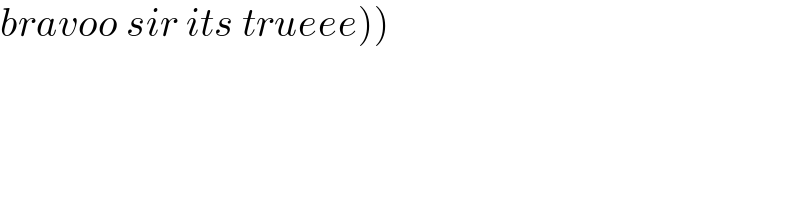
$$\left.{b}\left.{ravoo}\:{sir}\:{its}\:{trueee}\right)\right) \\ $$
Commented by mindispower last updated on 18/Oct/21
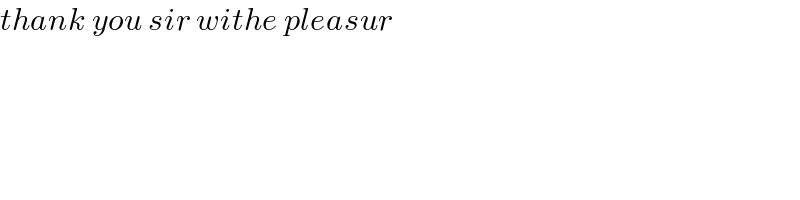
$${thank}\:{you}\:{sir}\:{withe}\:{pleasur} \\ $$
