
Question Number 35949 by ajfour last updated on 26/May/18
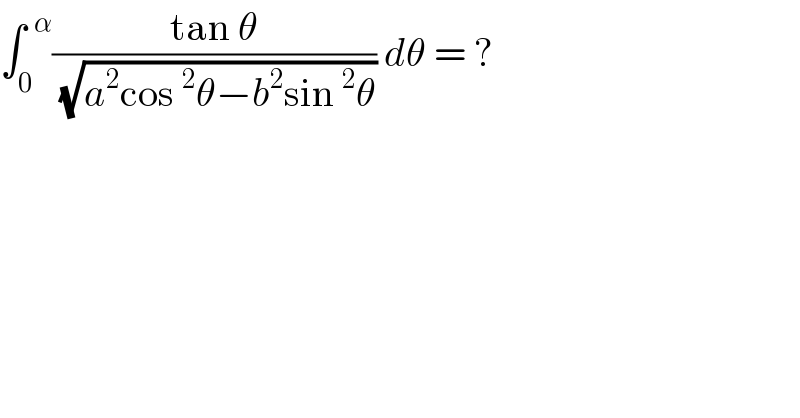
$$\int_{\mathrm{0}} ^{\:\:\alpha} \frac{\mathrm{tan}\:\theta}{\sqrt{{a}^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta−{b}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta}}\:{d}\theta\:=\:? \\ $$
Commented by abdo mathsup 649 cc last updated on 26/May/18
![let put I_α = ∫_0 ^α ((tanθ)/(√(a^2 cos^2 θ−b^2 sin^2 θ)))dθ we hsve the formula 1+tan^2 θ =(1/(cos^2 θ)) ⇒ cos^2 θ = (1/(1+tan^2 θ)) and sin^2 θ =1−(1/(1+tan^2 θ)) ⇒ a^2 cos^2 θ −b^2 sin^2 θ = (a^2 /(1+tan^2 θ)) −b^2 ((tan^2 θ)/(1+tan^2 θ)) = ((a^2 −b^2 tan^2 θ)/(1+tan^2 θ)) ⇒ I_α = ∫_0 ^α ((tanθ(√(1+tan^2 θ)))/(√(a^2 −b^2 tan^2 θ))) dθ changement tanθ =t give I_α = ∫_0 ^(tanα) ((t(√(1+t^2 )))/(√(a^2 −b^2 t^2 ))) (dt/(1+t^2 )) = ∫_0 ^(tan(α)) (t/(√(1+t^2 ))) (dt/(√(a^2 −b^2 t^2 ))) by parts u^′ = (t/(√(1+t^2 ))) and v = (1/(√(a^2 −b^2 t^2 ))) I_α = [ ((√(1+t^2 ))/(√(a^2 −b^2 t^2 )))]_0 ^(tan(α)) −∫_0 ^(tan(α)) (√(1+t^2 )) (−(1/2)−2b^2 t)(a^2 −b^2 t^2 )^(−(3/2)) dt =((√(1+tan^2 α))/(√(a^2 −b^2 tan^2 α))) − (1/(∣a∣)) −b^2 ∫_0 ^(tan(α)) (√(1+t^2 ))( a^2 −b^2 t^2 )^(−(3/2)) dt let J = ∫_0 ^(tan(α)) (√(1+t^2 )) (a^2 −b^2 t^2 )^(−(3/2)) dt =c ∫_0 ^(tan(α)) ((√(1+t^2 ))/((a^2 −b^2 t^2 )(√(a^2 −b^2 t^2 ))))dt ...be continued ...](Q35970.png)
$${let}\:{put}\:{I}_{\alpha} \:=\:\int_{\mathrm{0}} ^{\alpha} \:\:\:\frac{{tan}\theta}{\sqrt{{a}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta−{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta}}{d}\theta\: \\ $$$${we}\:{hsve}\:{the}\:{formula}\:\:\mathrm{1}+{tan}^{\mathrm{2}} \theta\:=\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\:\Rightarrow \\ $$$${cos}^{\mathrm{2}} \theta\:=\:\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:\:{and}\:\:{sin}^{\mathrm{2}} \theta\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:\Rightarrow \\ $$$${a}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\:−{b}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta \\ $$$$=\:\frac{{a}^{\mathrm{2}} }{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:−{b}^{\mathrm{2}} \:\:\frac{{tan}^{\mathrm{2}} \theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:=\:\frac{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} \:{tan}^{\mathrm{2}} \theta}{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\:\Rightarrow \\ $$$${I}_{\alpha} \:=\:\int_{\mathrm{0}} ^{\alpha} \:\frac{{tan}\theta\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {tan}^{\mathrm{2}} \theta}}\:{d}\theta\:\:{changement}\:{tan}\theta\:={t} \\ $$$${give}\:{I}_{\alpha} \:=\:\:\int_{\mathrm{0}} ^{{tan}\alpha} \:\:\:\:\frac{{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} }}\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{{tan}\left(\alpha\right)} \:\:\:\:\frac{{t}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:\:\:\frac{{dt}}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} }}\:\:{by}\:{parts} \\ $$$${u}^{'} \:=\:\frac{{t}}{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:{and}\:\:{v}\:=\:\frac{\mathrm{1}}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} }}\:\: \\ $$$${I}_{\alpha} \:\:=\:\left[\:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} }}\right]_{\mathrm{0}} ^{{tan}\left(\alpha\right)} −\int_{\mathrm{0}} ^{{tan}\left(\alpha\right)} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}{b}^{\mathrm{2}} {t}\right)\left({a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} {dt} \\ $$$$=\frac{\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \alpha}}{\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} \:{tan}^{\mathrm{2}} \alpha}}\:−\:\frac{\mathrm{1}}{\mid{a}\mid}\:\:−{b}^{\mathrm{2}} \:\int_{\mathrm{0}} ^{{tan}\left(\alpha\right)} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\left(\:{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} {dt} \\ $$$${let}\:{J}\:=\:\int_{\mathrm{0}} ^{{tan}\left(\alpha\right)} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:\left({a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} {dt} \\ $$$$={c}\:\int_{\mathrm{0}} ^{{tan}\left(\alpha\right)} \:\:\:\:\frac{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}{\left({a}^{\mathrm{2}} \:\:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} \right)\sqrt{{a}^{\mathrm{2}} \:−{b}^{\mathrm{2}} {t}^{\mathrm{2}} }}{dt}\:\:...{be}\:{continued}\:... \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 26/May/18

$$\int_{\mathrm{0}} ^{\alpha} \frac{{tan}\theta.{sec}\theta}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} {tan}^{\mathrm{2}} \theta}}{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\alpha} \frac{{tan}\theta{sec}\theta}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} {sec}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} }}{d}\theta \\ $$$$\frac{\mathrm{1}}{{b}}\int\frac{{d}\left({sec}\theta\right)}{\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} }−{sec}^{\mathrm{2}} \theta}} \\ $$$${now}\:{use}\:{formula}\:\int\frac{{dx}}{\sqrt{{A}^{\mathrm{2}} −{X}^{\mathrm{2}} }} \\ $$$$\frac{\mathrm{1}}{{b}}×\mid{sin}^{−\mathrm{1}} \left(\frac{{sec}\theta}{\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}}\right)\mid_{\mathrm{0}} ^{\alpha} \\ $$$$\frac{\mathrm{1}}{{b}}×\left\{{sin}^{−\mathrm{1}} \left(\frac{{sec}\alpha}{\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{b}^{\mathrm{2}} }}}\right)−{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{{b}^{\mathrm{2}} }}\right)\right\} \\ $$
Commented by ajfour last updated on 26/May/18

$${Thanks}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 26/May/18

$${its}\:{ok}... \\ $$
Commented by ajfour last updated on 26/May/18

$${i}\:{applied}\:{your}\:{technique}\:{again} \\ $$$${and}\:{corrected}\:{my}\:{answer}\:{to} \\ $$$${Q}.\mathrm{35940}\:.\:{Thanks}\:{again}. \\ $$
