
Question Number 160415 by amin96 last updated on 29/Nov/21
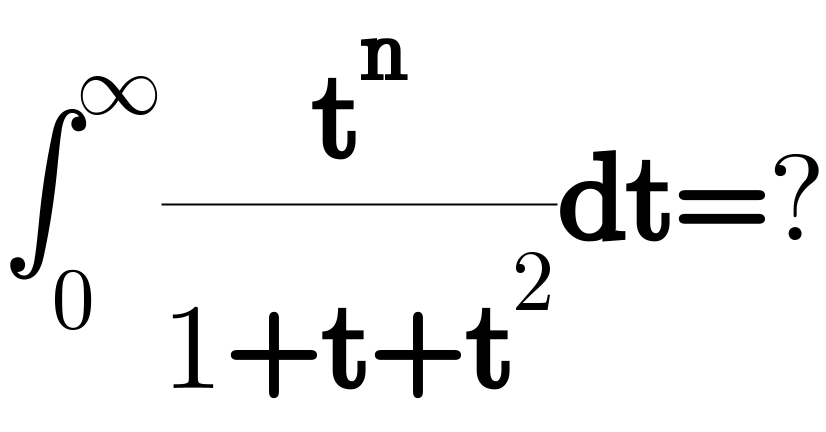
$$\int_{\mathrm{0}} ^{\infty} \frac{\boldsymbol{\mathrm{t}}^{\boldsymbol{\mathrm{n}}} }{\mathrm{1}+\boldsymbol{\mathrm{t}}+\boldsymbol{\mathrm{t}}^{\mathrm{2}} }\boldsymbol{\mathrm{dt}}=? \\ $$
Answered by MJS_new last updated on 29/Nov/21
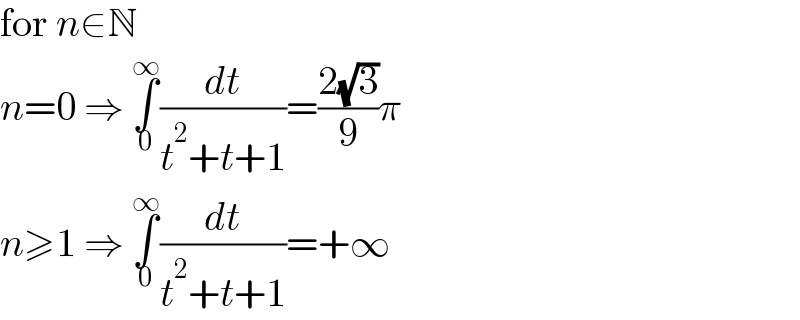
$$\mathrm{for}\:{n}\in\mathbb{N} \\ $$$${n}=\mathrm{0}\:\Rightarrow\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}=\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{9}}\pi \\ $$$${n}\geqslant\mathrm{1}\:\Rightarrow\:\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}=+\infty \\ $$
Commented by amin96 last updated on 29/Nov/21

$$\int\frac{\boldsymbol{\mathrm{t}}^{\boldsymbol{\mathrm{n}}} }{\mathrm{1}+\boldsymbol{\mathrm{t}}+\boldsymbol{\mathrm{t}}^{\mathrm{2}} }\boldsymbol{\mathrm{dt}}=?\: \\ $$so when
